概念:换元法是数学中一个非常重要而且应用十分广泛的解题方法。我们通常把未知数或变数称为元,所谓换元法,就是在一个比较复杂的数学式子中,用新的变元去代替原式的一个部分或改造原来的式子,使它简化,使问题易于解决。
经验:换元法,可以运用于因式分解、解方程或方程组等方面。换元法是数学中重要的解题方法,对于一些较繁较难的数学问题,若能根据问题的特点,进行巧妙的换元,则可以收到事半功倍的效果,现举例说明.
详解:换元法主要有双换元、整体换元、均值换元,倒数换元几种形式。下面结合例题一一讲解。
1.整体换元

2.双换元

3.均值换元

4.系数对称方程换元

5. 倒数换元
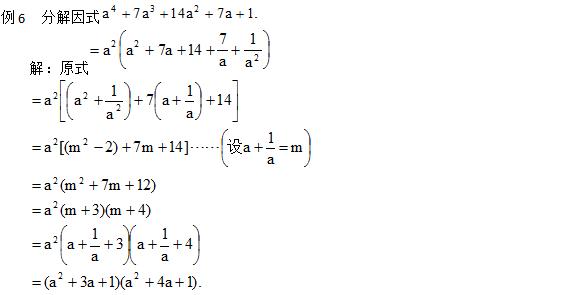
 加载中,请稍侯......
加载中,请稍侯......
精彩评论