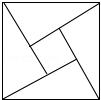
1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)²=21,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
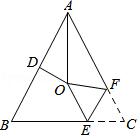
2.(2018秋•鄂州期末)如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
A.106° B.108° C.110° D.112°
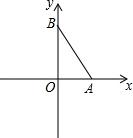
3.如图,在平面直角坐标系中,点A,B分别在x轴,y轴上,且∠ABO=30°,点P在坐标轴上且使△ABP为等腰三角形,则满足条件的点P共有_________个.
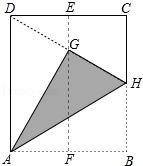
4.如图,在一张矩形纸片ABCD中,AD=4 cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,且DG=GH,则CD的长为_________.
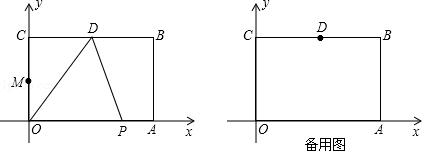
5。如图,在平面直角坐标系中,长方形OABC的顶点A,B的坐标分别为A(6,0),B(6,4),D是BC的中点,动点P从O点出发,以每秒1个单位长度的速度,沿着O→A→B→D运动,设点P运动的时间为t秒(0<t<13).
(1)①点D的坐标是(______,_________);
②当点P在AB上运动时,点P的坐标是(________,__________)(用t表示);
(2)写出△POD的面积S与t之间的函数关系式,并求出△POD的面积等于9时点P的坐标;
(3)当点P在OA上运动时,连接BP,将线段BP绕点P逆时针旋转,点B恰好落到OC的中点M处,则此时点P运动的时间t=________秒.(直接写出答案)
答案与解析





 加载中,请稍侯......
加载中,请稍侯......
精彩评论