全等三角形中的动点问题

步骤总结（见例一）：①找到相等角（∠A=∠B）

②固定一个三角形的字母顺序（△APC）

③将另一个三角形的字母顺序对应写出全等（△APC≌△BPQ或△APC≌△BQP）

④得出对应边相等（对应边一定是从等角出发的边，即AP=BP,AC=BQ或AP=BQ,AC=BP）

⑤用数字或字母表示出这些边，并计算出结果。

注意：相等的角的位置必须对应，将两外两个字母顺序互换即得到两种情况。

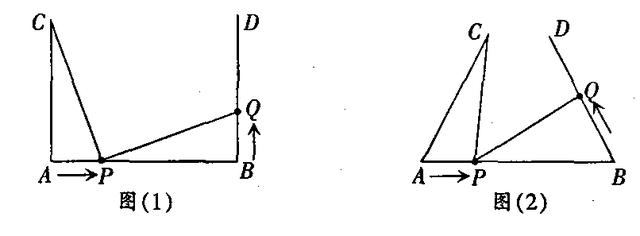
例1:如图(1)，AB＝4cm，AC⊥AB，BD⊥AB，AC＝BD＝3cm．点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t(s)．

(1)若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系__________；

(2)如图(2)，将图(1)中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变．设点Q的运动速度为x cm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由．

练一练：

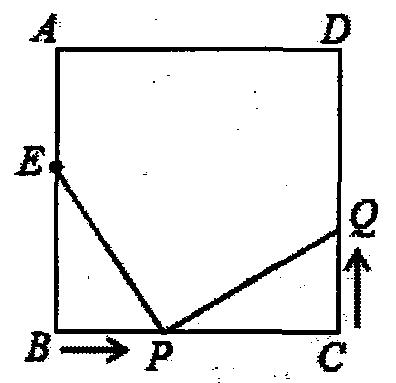
例二:如图，已知正方形ABCD中，边长为10cm，点E在AB边上，BE＝6cm．

(1)如果点P在线段BC上以4cm/秒的速度由B点向C点运动，同时，点Q在线段CD上以acm/秒的速度由C点向D点运动，设运动的时间为t秒，

①CP的长为_______cm（用含t的代数式表示）；

②若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等，求a的值．

(2)若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿正方形ABCD四边运动．则点P与点Q会不会相遇？若不相遇，请说明理由．若相遇，求出经过多长时间点P与点Q第一次在正方形ABCD的何处相遇？

例二答案