九年级数学（上）期中复习每日一练（10月25日）

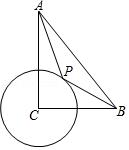
1．如图，在Rt△ABC中，∠ACB＝90°，CB＝7，AC＝9，以C为圆心、3为半径作⊙C，P为⊙C上一动点，连接AP、BP，则1/3AP+BP的最小值为（ ）

A．7 B．5√2 C．4+√10 D．2√13

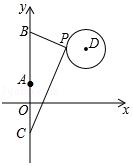
2．如图，在平面直角坐标系中，已知点A（0，1）、点B（0，1+t）、C（0，1﹣t）（t＞0），点P在以D（3，3）为圆心，1为半径的圆上运动，且始终满足∠BPC＝90°，则t的最小值是（ ）

A．√13-1 B．5 C．4 D．√3+1

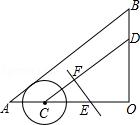
3．如图，△AOB中，∠O＝90°，AO＝8cm，BO＝6cm，点C从A点出发，在边AO上以2cm/s的速度向O点运动，与此同时，点D从点B出发，在边BO上以1.5cm/s的速度向O点运动，过OC的中点E作CD的垂线EF，则当点C运动了________s时，以C点为圆心，1.5cm为半径的圆与直线EF相切．

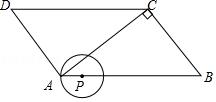
4．如图，平行四边形ABCD中，AC⊥BC，AB＝5，BC＝3，点P在边AB上运动，以P为圆心，PA为半径作⊙P，若⊙P与平行四边形ABCD的边有四个公共点，则AP的长度的取值范围是_________．

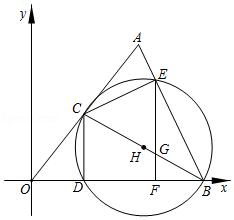
5．如图，在平面直角坐标系中，A（3，4），B（5，0），连接AO．AB点C是线段AO上的动点（不与A，O重合）连结BC，以BC为直径作⊙H，交x轴于点D，交AB于点E，连接CD、CE，过E作EF⊥x轴于F，交BC于G．

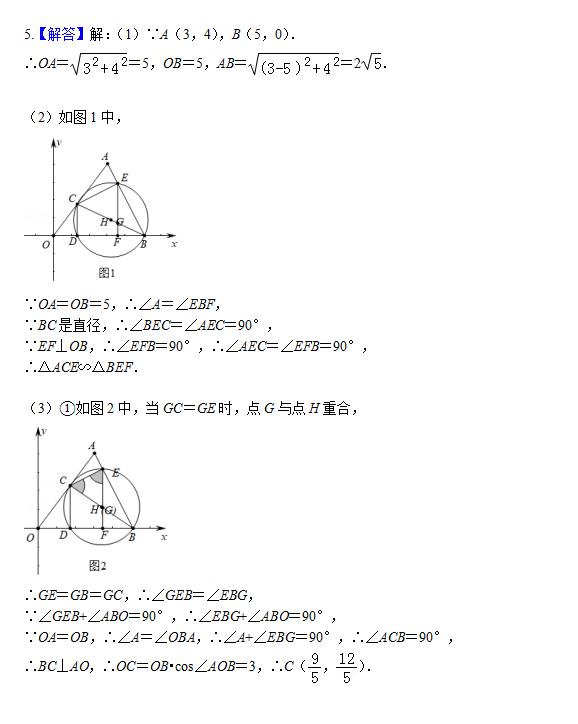
（1）求AO和AB的长；

（2）求证：△ACE∽△BEF；

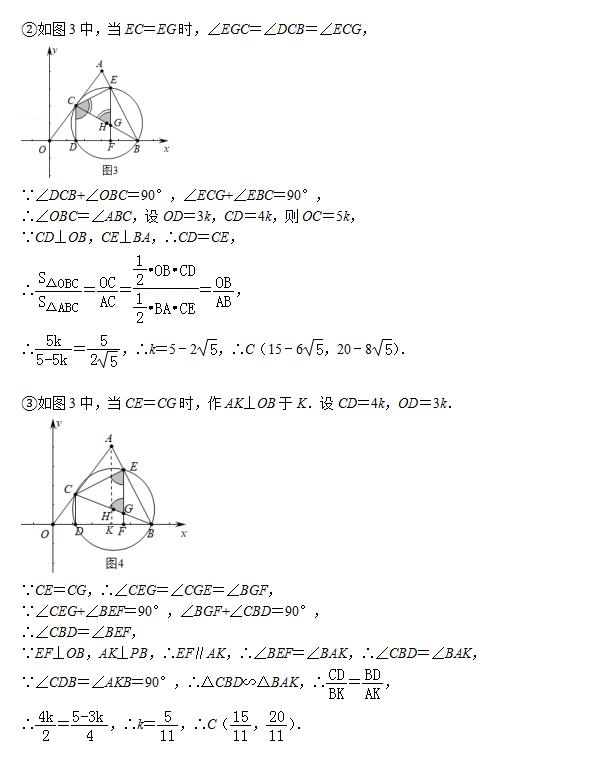
（3）若△CEG是等腰三角形，求C点坐标．

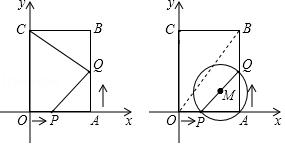
6.如图，四边形OABC是矩形，点A的坐标为（3，0），点C的坐标为（0，6），点P从点O出发，沿OA以每秒1个单位长度的速度向点A出发，同时点Q从点A出发，沿AB以每秒2个单位长度的速度向点B运动，当点P与点A重合时运动停止．设运动时间为t秒．

（1）当t＝2时，线段PQ的中点坐标为 ．

（2）当△CBQ与△PAQ相似时，求t的值；

（3）连接OB，若以PQ为直径作⊙M，则在运动过程中，是否存在某一时刻t，使得⊙M与OB相切，若存在，求出时间t；若不存在，请说明理由．

答案与解析