一题多解，数学思想的完美体现

题目： 如图1，点F是正方形ABCD的边CD上一点，以点A为圆心、AB为半径的弧与BF交于点E，则∠DEF=_________．

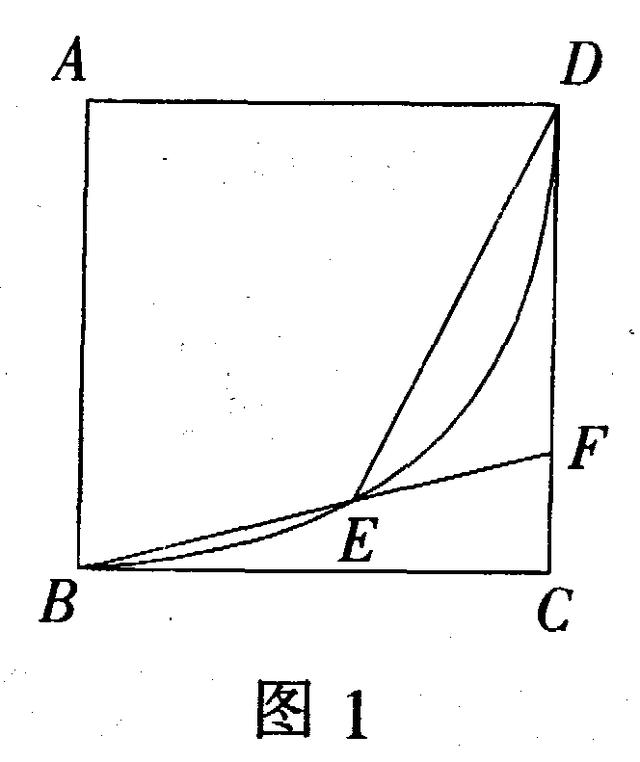
一．运用方程思想

解法1 如图2，连结AE，则AB=AE=AD．

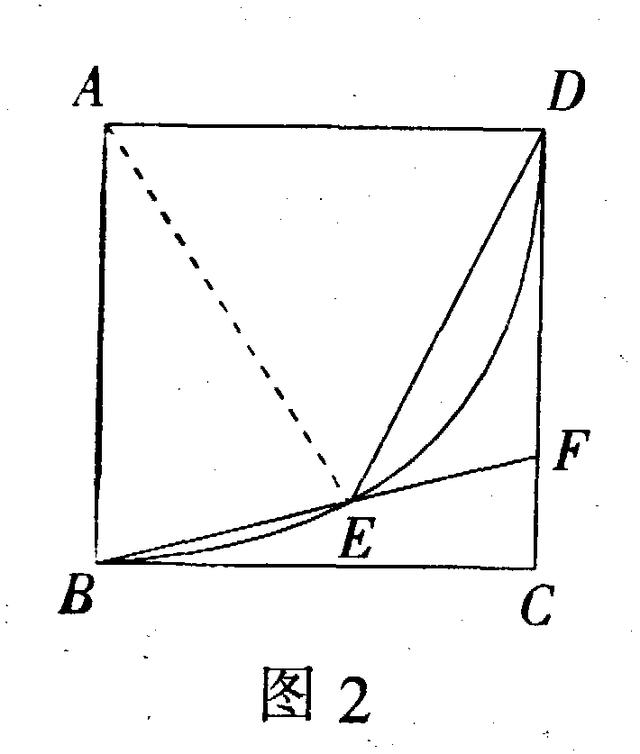
设∠AEB=x，∠AED=y，则∠ABE=∠AEB=y， ∠ADE=∠AED=y，

∴∠BAE+∠DAE = 1/2(180°) =90°

可得， 即∠BED=135°， ∴∠DEF=45°．

解法2 如图3，作AP⊥BE于点P，作A Q⊥ED于点Q．

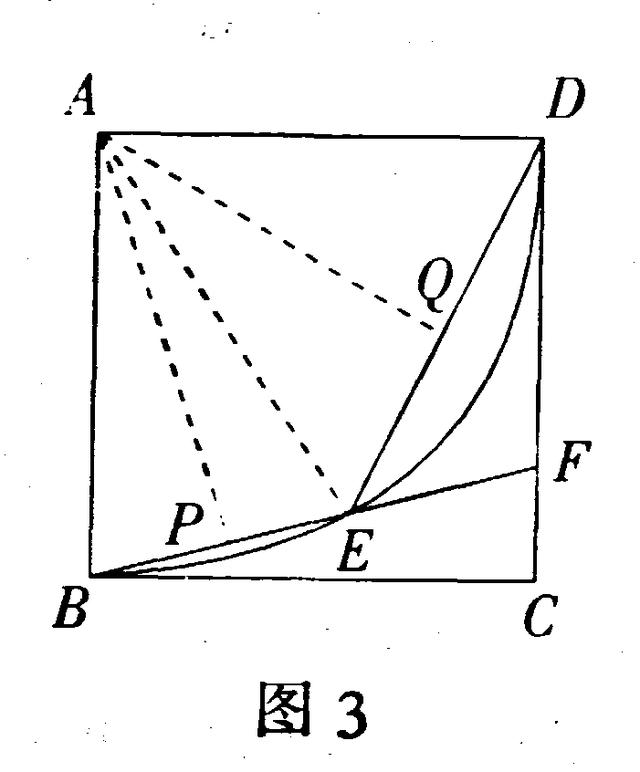
根据垂径定理，BP=PE，EQ=QD，

故可设∠BAP=∠PAE=m。

∠DA Q=∠QAE=n．

由∠BAD=90°，得m+n=45°，即∠PA Q=45°，

∴∠BED=135°， ∴∠DEF=45°．

点评 两种解法，都是运用字母表示数，根据相关条件找出等量关系，体现了方程思相事实上，这里没有求出相应未知数的值，这又体现了整体思想．

二．运用特殊化思想

解法3 如图4，连结AC，交弧BD于点E，连BE并延长交CD于点F，连DE．

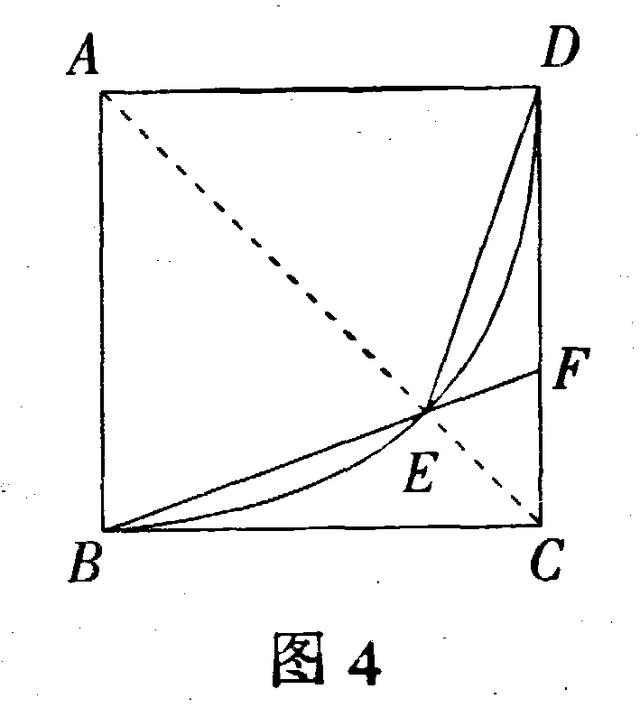
∵AB=AE=AD， ∠BAE=∠DAE=45°，

∴∠ BEA=∠DEA=67.5°． 即∠BED=135°， ∴∠DEF=45°．

点评 因为F是CD上的任意一点，当然包括某个特殊情形，所以本解法适当改变了图形，采用了点F的特殊位置．解有关数学填空或选择题，采用特别数值或特殊位置等，是常见的一些比较好的思想方法．

三．运用圆周角定理

解法4 如图5，连结AE、BD，根据圆周角定理，得

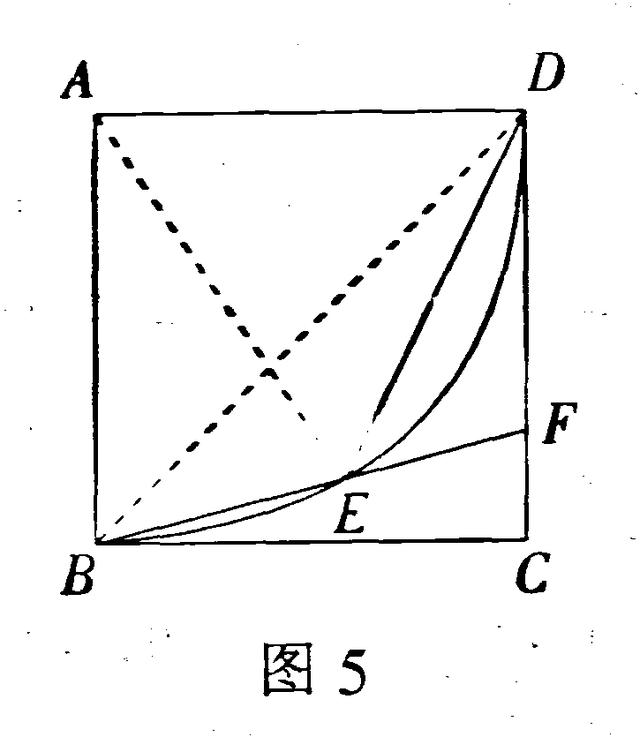
∠BDE=½∠BAE，∠ DBE=½∠DAE，

∴∠DEF=∠DBE+∠BDE =½∠BAD=45º．

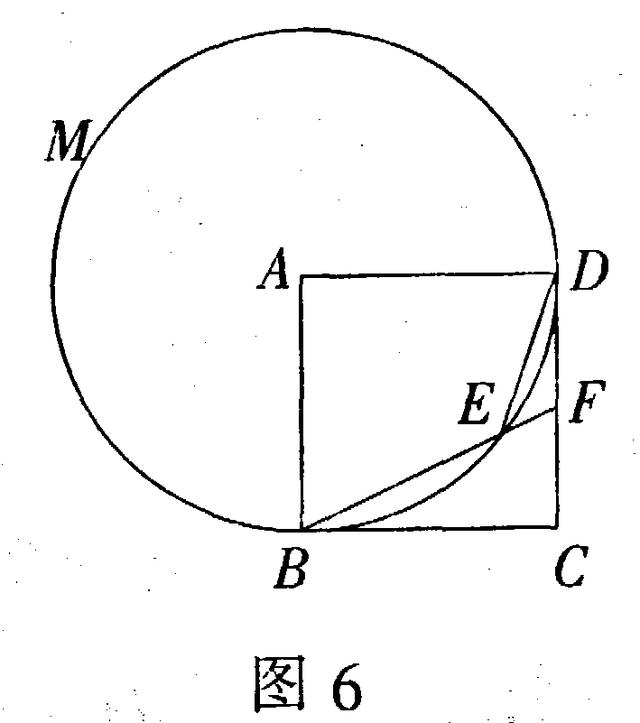
解法5 如图6，补全圆A，则优弧BMD所对的圆心角270°，所以圆周角∠BED=

135°，从而∠DEF=45°．

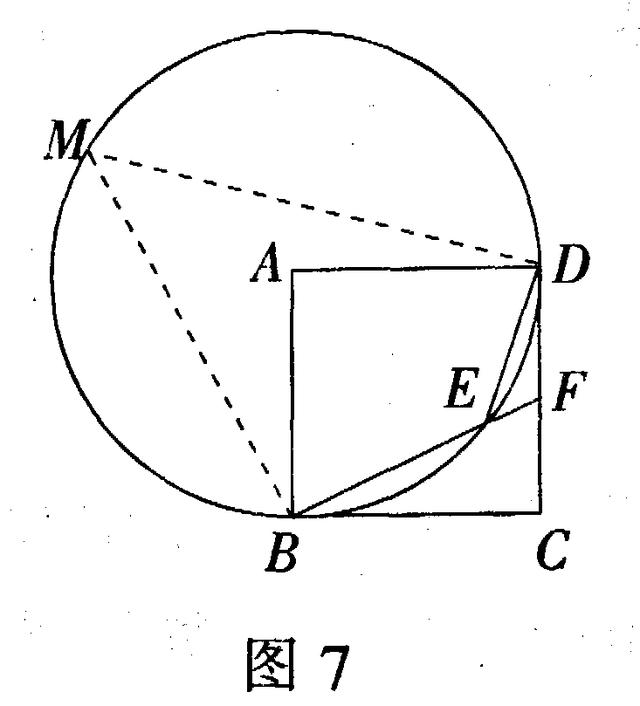
解法6 如图7，在优弧上任取一点M，连接．MD、MB，根据圆周角定理，AM=45°．四边形BMDE是圆A的内接四边形，再根据圆内接四边性质，∠DEF=∠M=45°．

点评 圆周角，是《圆》的核心内容之一，所以很自然地想到运用圆周角定理．事实上，在解法5和解法6里，又都体现了补全思想，很巧妙．