三角形全等的简单应用

【典型例题】

一．生活中的应用

例题1：如图，两根长12m的绳子，一端系在旗杆上的同一位置，另一端分别固定在地面上的两个木桩上（绳结处的误差忽略不计），现在只有一把卷尺，如何来检验旗杆是否垂直于地面？请说明理由．

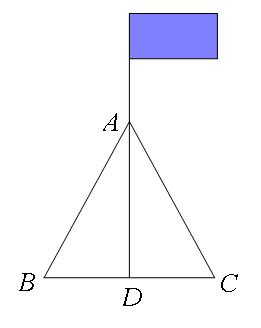
二．运动型问题中的应用

例题2：如图，AB＝6cm，AC＝BD＝4cm．∠CAB＝∠DBA，点P在线段AB上以2cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．设点Q的运动速度为xcm/s，若使得△ACP与△BPQ全等，则x的值为____________．

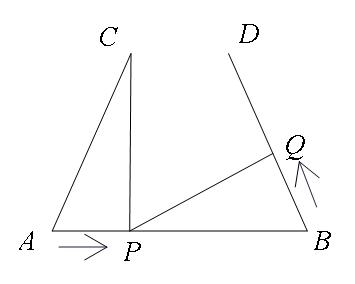
三．全等应用的几个重要模型

(1)中线型

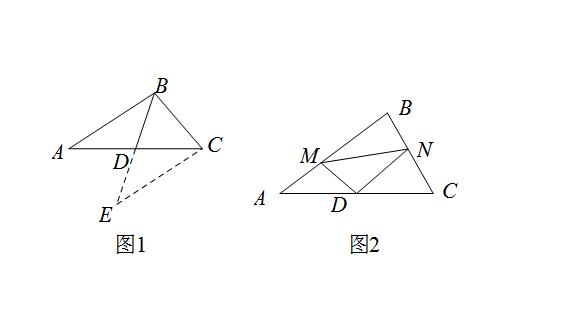
例题3:（1）阅读理解：如图1，在△ABC中，若AB＝10，BC＝8．求AC边上的中线BD的取值范围．

小聪同学是这样思考的：延长BD至E使DE＝BD，连结CE.利用全等将边AB转化到CE，在△BCE中利用三角形三边关系即可求出中线BD的取值范围．在这个过程中小聪同学证三角形全等用到的判定方法是__________；中线BD的取值范围是_____________．

（2）问题解决：如图2，在△ABC中，点D是AC的中点，点M在AB边上，点N在BC边上，若DM⊥DN．求证：AM+CN＞MN．

(2)角平分线型

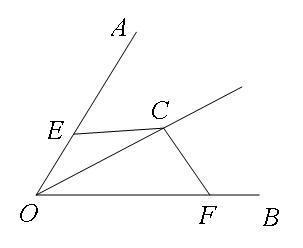
例题4:如图，已知OC平分∠AOB，点E、F分别在边OA、OB上，且EC=FC．若∠AOB=60°，求∠ECF的度数；

(3)K型全等

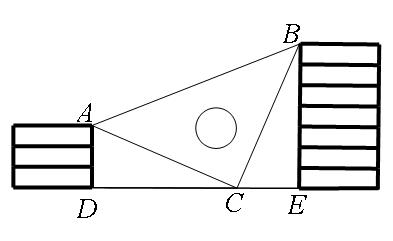
例题5:王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC＝BC，∠ACB＝90°），点C在DE上，点A和B分别与木墙的顶端重合，求两堵木墙之间的距离．

以上五种题型一定要熟练掌握