折叠问题中所包含的勾股定理的运用

折叠问题是中考的热点也是难点问题，通常与动点问题结合起来，这类问题的题设通常是将某个图形按一定的条件折叠，通过分析折叠前后图形的变换，借助轴对称性质、勾股定理等知识进行解答。

此类问题立意新颖，充满着变化，要解决此类问题，除了能根据轴对称图形的性质作出要求的图形外，还要能综合利用相关数学模型及方法来解答。

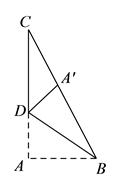
例1. 如图1-1，在Rt△ABC中，∠A=90°，AB=3，AC=4，现将△ABC沿BD进行翻折，使点A刚好落在BC上，则CD=__________．

例2. 如图，长方形ABCD中，AB=3，BC=4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处．当△CEB′为直角三角形时，BE的长为________．

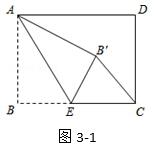
【点睛】本题解题关键在准确对问题进行分类讨论，并作出相应图形利用折叠的性质及勾股定理解题.

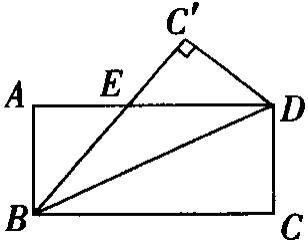
例3. 如图，在长方形ABCD中，将△DBC沿BD对折至△DBC’位置，BC’与AD交于点E.

（1）试说明：BE=DE；（2）如果AB=6，BC=8，求△EBD的面积.

例4. 动手操作：在矩形纸片ABCD中，AB=3，AD=5. 如图所示，折叠纸片，使点A落在BC边上的A’处，折痕为PQ，当点A’在BC边上移动时，折痕的端点P、Q也随之移动. 若限定点P、Q分别在AB、AD边上移动，则点A’在BC边上可移动的最大距离为 __________.

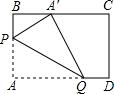
【点睛】此题难度较大，主要考察学生的分析能力，作图能力。作图的依据是折叠前后线段长度不变，先找到点A的落点A'，再根据对称轴（折痕）是对应点连线的垂直平分线，确定出折痕PQ的位置. 利用勾股定理、正方形的判定定理及其性质求得相应的线段长度.