九年级压轴题型：几何动点问题探究

1．如图．A、B、C、D为矩形的4个顶点：AB＝16cm，BC＝6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达点B为止：点Q以2cm/s的速度向点B移动，经过多长时间P、Q两点之间的距离是10cm？

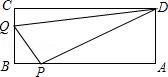
【分析】设P，Q两点从出发经过t秒时，点P，Q间的距离是10cm，表示出PB、BQ，利用勾股定理建立方程求得答案即可．

【点评】考查一元二次方程的应用；利用勾股定理得到等量关系是解决本题的关键．

2．已知：Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点E在AC上（E与A、C均不重合）．

（1）若点F在AB上，且EF平分Rt△ABC的周长，设AE＝x，用含x的代数式表示△AEF的面积S△AEF；

（2）若点F在折线ABC上移动，试问是否存在直线EF将Rt△ABC的周长与面积同时平分？若存在直线EF，则求出AE的长；若不存在，请说明理由．

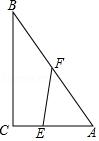
【分析】（1）根据AE＝x得到AF，然后表示出DF，利用三角形的面积列出两个变量之间的关系式即可；

（2）根据EF平分三角形ABC的面积列出有关x的一元二次方程，解得有意义即可判定存在．

【点评】本题考查了一元二次方程的应用及根据实际问题列出二次函数关系式，解题的关键是根据已知条件表示出有关的线段的长．

3．如图，在矩形ABCD中，AB＝16cm，BC＝6cm，点P从点A出发，以3cm/s的速度向点B移动，一直到达点B为止；同时，点Q从点C出发，以2cm/s的速度向点D移动．当其中一个点停止移动时，另一个点也随之停止，设移动时间为ts，连接PQ．

（1）当t＝2时，求PQ的长；

（2）当PQ＝10cm时，求t的值．

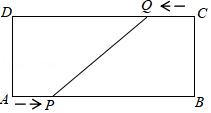
【分析】（1）作QH⊥AB，垂足为H，则QH＝BC＝6，根据题意求得BH＝QC＝4cm，即可求得PH＝AB﹣AP﹣BH＝16﹣6﹣4＝6cm，然后根据勾股定理求得即可；

（2）设运动时间为t秒，用t表示线段长，用勾股定理列方程求解．

【点评】此题考查了一元二次方程的运用．利用作垂线，构造直角三角形，运用勾股定理列方程是解题关键．