初二数学经典的做对称求最小值问题，也是中考中的常客

做对称求最小值问题常见的三种提问方式：①直接求一条线段AB的最小值②求两条线段AB+AC和的最小值③求三条线段构成的三角形ABC的周长的最小值

接下来我们用几道例题来分析一下这几种类型。

方法总结（以例1为例）：①将C,F,E三点分为动点和定点（其中c为定点，E,F为动点）

②找到动点运动的轨迹（F在AD上运动，E在AC上运动）

③将定点沿着动点的运动轨迹对对称（将点C沿着AD做对称至B点）

④从对称点出发做一条与另一运动轨迹相垂直的直线（从点B做BE⊥AC）

⑤算出所作出的直线的长度即为最小值（算出BE的长度）

一、求两条线段AB+AC和的最小值

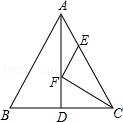
例1、如图，△ABC中，AB＝AC＝13，BC＝10，AD是BC边上的中线且AD＝12，F是AD上的动点，E是AC边上的动点，则CF+EF的最小值为___________．

二、直接求一条线段AB的最小值

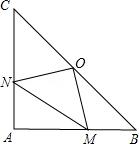
例2、如图，在△ABC中，∠A＝90°，AB＝AC，O是BC的中点，如果在AB和AC上分别有一个动点M、N在移动，且在移动时保持AN＝BM．

（1）请你判断△OMN的形状，并说明理由．

（2）若BC＝2√2，则MN的最小值为__________.

三、三条线段构成的三角形ABC的周长的最小值．

常考的题型解法：将 △ABC的周长拆成AB+AC+BC,其中一定会有一条边的长度是已知的，若AB的长为3，那么△ABC的周长的最小值就是在求3+AC+BC的最小值，接下来的步骤与例题1相同。