中考压轴题：与圆相关的最值问题

例1：如图，⊙O是以原点为圆心，2为半径的圆，点P是直线y＝﹣x+4上的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为________．

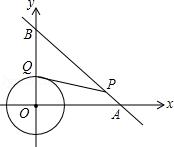
【分析】先根据坐标轴上点的坐标特征确定B（0，4）,A（4，0），则可判断△OAB为等腰直角三角形，所以AB＝√2,OA＝4√2，OH＝1/2AB＝2√2，再根据切线的性质，由PQ为⊙O的切线得到OQ⊥PQ，根据勾股定理得到PQ＝√op²-OQ²＝√OP²-4，所以当OP最小时，PQ最小，根据垂线段最短得到OP＝OH时，OP最小，即可计算出切线长PQ的最小值＝2．

【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．也考查了一次函数图象上点的坐标特征．

例2：如图，在平面直角坐标系中，已知点A（0，1）、点B（0，1+t）、C（0，1﹣t）（t＞0），点P在以D（3，3）为圆心，1为半径的圆上运动，且始终满足∠BPC＝90°，则t的最小值是_____．

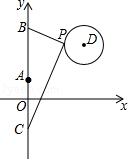
【分析】先求出AB，AC进而得出AC＝AB，结合直角三角形的斜边的中线等于斜边的一半，即AP＝t，即可得出t最小时，点P在AD上，用两点间的距离公式即可得出结论．

【点评】此题主要考查了直角三角形斜边的中线的性质，平面坐标系内，两点间的距离公式，极值的确定；判断出点A是BC的中点是解本题的关键．是一道基础题．

例3：如图，在Rt△AOB中，OA＝OB＝3√2，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则线段PQ的最小值为_________.

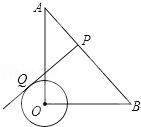
【分析】首先连接OP、OQ，根据勾股定理知PQ²＝OP²﹣OQ²，可得当OP⊥AB时，即线段PQ最短，然后由勾股定理即可求得答案．

【点评】本题考查了切线的性质、等腰直角三角形的性质以及勾股定理．此题难度适中，注意掌握辅助线的作法，注意得到当PO⊥AB时，线段PQ最短是关键．