初一数学：数轴上的动点题型研究

例一：已知，如图A、B分别为数轴上的两点，A点对应的数为﹣10，B点对应的数为70

（1）请写出AB的中点M对应的数

（2）现在有一只电子蚂蚁P从A点出发，以3个单位/秒的速度向右运动，同时另一只电子蚂蚁Q恰好从B点出发，以2个单位/秒的速度向左运动，设两只电子蚂蚁在数轴上的C点相遇，请你求出C点对应的数。

（3）若当电子蚂蚁P从A点出发，以3个单位/秒的速度向右运动，同时另一只电子蚂蚁Q恰好从B点出发，以2单位/秒的速度向左运动，经过多长时间两只电子蚂蚁在数轴上相距35个单位长度，并写出此时P点对应的数．

【分析】（1）求﹣10与70和的一半即是M对应的数；

（2）先求出AB的长，再设t秒后P、Q相遇即可得出关于t的一元一次方程，求出t的值，可求出P、Q相遇时点Q移动的距离，进而可得出C点对应的数；

（3）分为2只电子蚂蚁相遇前相距35个单位长度和相遇后相距35个单位长度，相遇前：（80﹣35）÷（2+3）＝9（秒），相遇后：（35+80）÷（2+3）＝23（秒）．

【点评】此题考查一元一次方程式为实际运用，利用行程问题的基本数量关系，以及数轴直观解决问题即可．

例二：如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．

（1）数轴上点B表示的数是_______，点P表示的数是______（用含t的代数式表示）；

（2）动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发．求：

①当点P运动多少秒时，点P与点Q相遇？

②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？

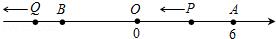
【分析】（1）由已知得OA＝6，则OB＝AB﹣OA＝4，因为点B在原点左边，从而写出数轴上点B所表示的数；动点P从点A出发，运动时间为t（t＞0）秒，所以运动的单位长度为6t，因为沿数轴向左匀速运动，所以点P所表示的数是6﹣6t

（2）①点P运动t秒时追上点Q，由于点P要多运动10个单位才能追上点Q，则6t＝10+4t，然后解方程得到t＝5；

②分两种情况：当点P运动a秒时，不超过Q，则10+4a﹣6a＝8；超过Q，则10+4a+8＝6a；由此求得答案解即可．

【点评】此题考查的知识点是两点间的距离及数轴，根据已知得出各线段之间的关系等量关系是解题关键．

例三：【探索新知】

如图1，点C将线段AB分成AC和BC两部分，若BC＝πAC，则称点C是线段AB的圆周率点，线段AC、BC称作互为圆周率伴侣线段．

（1）若AC＝3，则AB＝________.

（2）若点D也是图1中线段AB的圆周率点（不同于C点），则AC_____DB；（填“＝”或“≠”）

【深入研究】

如图2，现有一个直径为1个单位长度的圆片，将圆片上的某点与数轴上表示1的点重合，并把圆片沿数轴向右无滑动地滚动1周，该点到达点C的位置．

（3）若点M、N均为线段OC的圆周率点，求线段MN的长度．

（4）在图2中，若点D在射线OC上，且线段CD与图中以O、C、D中某两点为端点的线段互为圆周率伴侣线段，直接写出D点所表示的数．

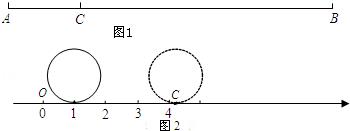
【分析】（1）根据线段之间的关系代入解答即可；

（2）根据线段的大小比较即可；

（3）由题意可知，C点表示的数是π+1，设M点离O点近，且OM＝x，根据长度的等量关系列出方程求得x，进一步得到线段MN的长度；

（4）根据圆周率伴侣线段的定义可求D点所表示的数．

【点评】考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．

例四：如图，已知一周长为30cm的圆形轨道上有相距10cm的A、B两点（备注：圆形轨道上两点间的距离是指圆上这两点间的较短部分展直后的线段长）．动点P从A点出发，以acm/s的速度，在轨道上逆时针方向运动，与此同时，动点Q从B点出发，以3cm/s的速度，按同样的方向运动，设运动时间为t（s），当t＝5时，动点P、Q第一次相遇．

（1）求a的值；

（2）若a＞3，则在P、Q第二次相遇前，当动点P、Q在轨道上相距12cm时，求t的值．

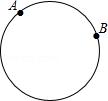
【分析】（1）根据相遇时，点P和点Q的运动的路程和等于AB的长列方程即可求解；

（2）设经过ts，P、Q两点相距12cm，分相遇前和相遇后两种情况建立方程求出其解；分点P，Q只能在直线AB上相遇，而点P旋转到直线AB上的时间分两种情况，所以根据题意列出方程分别求解．

【点评】此题考查一元一次方程的实际运用，掌握行程问题中的基本数量关系是解决问题的关键．