【考点1 一元二次方程的概念】
【方法点拨】解决此类问题掌握一元二次方程的定义是关键;等号两边都是整式,只含有一个未知数,并且未知数的最高次数是2的方程,叫做一元二次方程。

【思路点拨】根据一元二次方程的定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可.
【答案】解:①ax2+x+2=0,当a=0时,该方程属于一元一次方程,故错误;
②3(x﹣9)2﹣(x+1)2=1、④(a2+a+1)x2﹣a=0符合一元二次方程的定义,故正确;
③x+3=1/x属于分式方程,故错误;
⑤√x+1=x﹣1属于无理方程,故错误;
故选:B.
【点睛】此题主要考查了一元二次方程的定义,关键是掌握一元二次方程必须同时满足三个条件:①整式方程,即等号两边都是整式;方程中如果有分母,那么分母中无未知数; ②只含有一个未知数; ③未知数的最高次数是2.
【考点2 一元二次方程的解】
【方法点拨】一元二次方程的解(根)的意义:能使一元二次方程左右两边相等的未知数的值称为一元二次方程的解,解决此类问题,通常是将方程的根或解反代回去再进行求解.
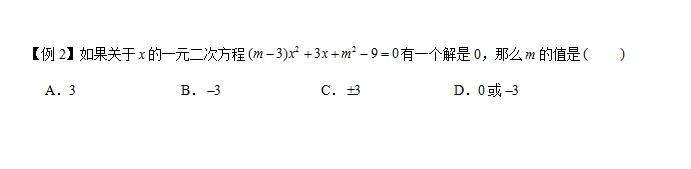
【思路点拨】把x=0代入方程(m﹣3)x²+3x+m²﹣9=0中,解关于m的一元二次方程,注意m的取值不能使原方程对二次项系数为0.
【答案】解:把x=0代入方程(m﹣3)x²+3x+m²﹣9=0中,得
m²﹣9=0,
解得m=﹣3或3,
当m=3时,原方程二次项系数m﹣3=0,舍去,
故选:B.
【点睛】本题考查的是一元二次方程解的定义.能使方程成立的未知数的值,就是方程的解,同时,考查了一元二次方程的概念.
【考点3 用指定方法解一元二次方程】
【方法点拨】解决此类问题需熟练掌握直接开方法、配方法、公式法、因式分解法的步骤.

【思路点拨】(1)方程变形后,利用平方根的定义开方即可求出解;
(2)方程常数项移到右边,两边加上一次项系数一半的平方,左边化为完全平方式,右边合并,开方即可求出解;
(3)方程整理为一般形式,找出a,b,c的值,当根的判别式大于等于0时,代入求根公式即可求出解;
(4)方程左边提取公因式化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.

【点睛】此题考查了解一元二次方程﹣因式分解法,配方法,公式法,以及直接开平方法,熟练掌握各自解法是解本题的关键.
【考点4 一元二次方程根的判别式】
【方法点拨】解决此类问题需熟练掌握根的判别式:当①b²-4ac>0时,方程有两个不相等的实数根;②b²-4ac=0时,方程有两个相等的实数根;③b²-4ac<0时,方程无实数根,反之亦成立.

【思路点拨】(1)根据一元二次方程根的判别式列出不等式,结合一元二次方程的定义可得a的范围;(2)将a的值代入得出方程,解之可得.
【答案】解:(1)由题意知△≥0,即4(a﹣1)²﹣4(a﹣2)(a+1)≥0,
解得:a≤3,∴a≤3且a≠2;
(2)由题意知a=3,
则方程为x2﹣4x+4=0,解得:x1=x2=2.
【点睛】本题考查的是根的判别式,熟知一元二次方程ax²+bx+c=0(a≠0)的根与△=b²﹣4ac的关系是解答此题的关键.
【考点5 一元二次方程根与系数的关系】
【方法点拨】解决此类问题需熟练掌根与系数的关系,熟记两根之和与两根之积,并且能够灵活运用所学知识对代数式进行变形得到两根之和与两根之积的形式,代入即可求值.

【思路点拨】(1)将所求的代数式进行变形处理:x₁²+x₂²=(x₁+x₂)²﹣2x₁x₂.
(2)根据异分母分式的加法法则进行变形处理,代入求值即可.

【点睛】此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
【考点6 有关一元二次方程传播问题】
【方法点拨】解有关一元二次方程的实际问题的一般步骤:
第1步:审题。认真读题,分析题中各个量之间的关系。
第2步:设未知数。根据题意及各个量的关系设未知数。
第3步:列方程。根据题中各个量的关系列出方程。
第4步:解方程。根据方程的类型采用相应的解法。
第5步:检验。检验所求得的根是否满足题意。
第6步:答。
【例6】今年春季某地区流感爆发,开始时有4人患了流感,经过两轮传染后,共有196人患了流感.若每轮每人传染的人数相同,求每轮每人传染的人数.
【思路点拨】设每轮传染的人数是x人,根据有4人患了流感,经过两轮传染后共有196人患了流感,列方程求解即可.
【答案】解:设每轮传染的人数是x人,根据题意得:
4x+4+(4x+4)x=196,
解得:x=6或x=﹣8(不合题意,舍去).
答:每轮传染的人数是6个人.
【点睛】此题考查了一元二次方程的应用,读懂题意,准确找到等量关系列出方程是解决问题的关键.此题要注意判断所求的解是否符合题意,舍去不合题意的解.
【考点7 有关一元二次方程面积问题】
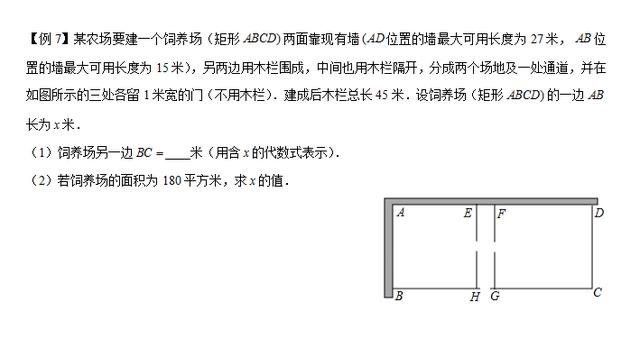
【思路点拨】(1)用(总长+2个2米的门的宽度)﹣3x即为所求;
(2)由(1)表示饲养场面积计算即可,
【答案】解:(1)由题意得:(48﹣3x)米.
故答案是:(48﹣3x);
(2)由题意得:x(48﹣3x)=180
解得x₁=6,x₂=10
【点睛】考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
【考点8 有关一元二次方程增长率问题】
【例8】 “美化城市,改善人民居住环境”是城市建设的一项重要内容.北京市将重点围绕城市副中心、大兴国际机场、冬奥会、世园会、永定河、温榆河、南中轴等重要节点区域绿化,到2022年,全市将真正形成一片集“万亩城市森林、百万乔灌树木、百种乡土植物、二十四节气林窗、四季景观大道”于一体的城市森林.2018年当年计划新增造林23万亩,2019年计划新增造林面积大体相当于27.8个奥森公园的面积,预计2020年计划新增造林面积达到38.87万亩,求2018年至2020年计划新增造林面积的年平均增长率.
【思路点拨】增长率问题,一般用增长后的量=增长前的量×(1+增长率)列出方程.
【答案】解:设2018年至2020年计划新增造林面积的年平均增长率为x,
根据题意得23(1+x)²=38.87,
解得x₁=0.3=30%,x₂=﹣2.3(不合题意,舍去).
答:2018年至2020年计划新增造林面积的年平均增长率为30%.
【点睛】此题主要考查了一元二次方程的应用,增长率问题,若原数是a,每次增长的百分率为x,则第一次增长后为a(1+x);第二次增长后为a(1+x)²,即原数×(1+增长百分率)²=后来数.
【考点9 有关一元二次方程利润问题】
【例9】某公司销售一种产品,进价为20元/件,售价为80元/件,公司为了促销,规定凡一次性购买10万件以上的产品,每多买1万件,每件产品的售价就减少2元,但售价最低不能低于50元/件,设一次性购买x万件(x>10)
(1)若x=15,则售价应是 元/件;
(2)一次性购买多少件产品时,该公司的销售总利润为728万元;

【考点10 有关一元二次方程动点问题】
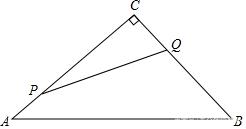
【例10】如图,在Rt△ABC中∠C=90º,AC=30cm,BC=21cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距15cm?△PCQ的面积能等于60平方厘米吗?为什么?


 加载中,请稍侯......
加载中,请稍侯......
精彩评论