例1:已知:如图,AD是△ABC的中线,求证:AB+AC>2AD.
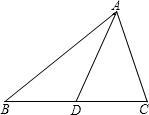
分析:本题是涉及两线段长度之和大于第三条线段长度的数量关系问题,应该想到,放在三角形的三边关系来考虑.而这里的AD为中线,要构造2AD,显然要延长中线AD,即倍长中线.
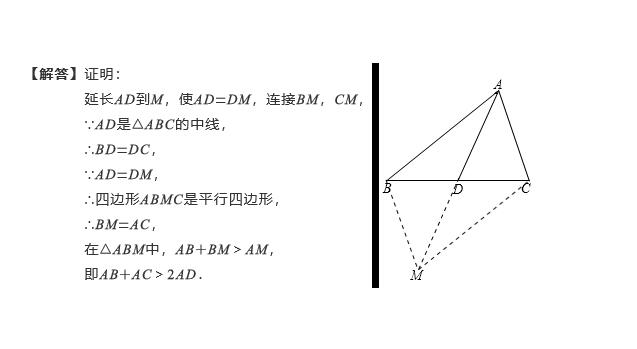
例2:△ABC中,D为BC中点,已知AB=7,AD=5,求AC的取值范围.
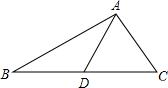
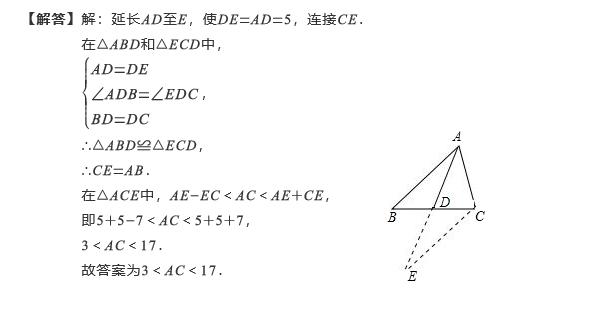
例3:如图,△ABC 中,D是BC的中点,DE⊥DF,请判断BE,CF,EF之间的数量关系.
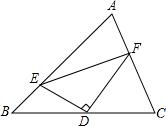
分析:本题中,要直接发现BE,EF,CF 间的大小关系很困难,三条线段不在同一个三角形中.受上一题启发,可能有同学会想到连接AD,倍长中线.但是,这样只能将AC转化至某一条线段,与CF没有关系.因此看到中点D,我们也要想到倍长与中点相关的线段FD.再联想到∠EDF=90°,想到通过二次全等,转化EF,以达到将三条线段转化至同一个三角形内的目的.
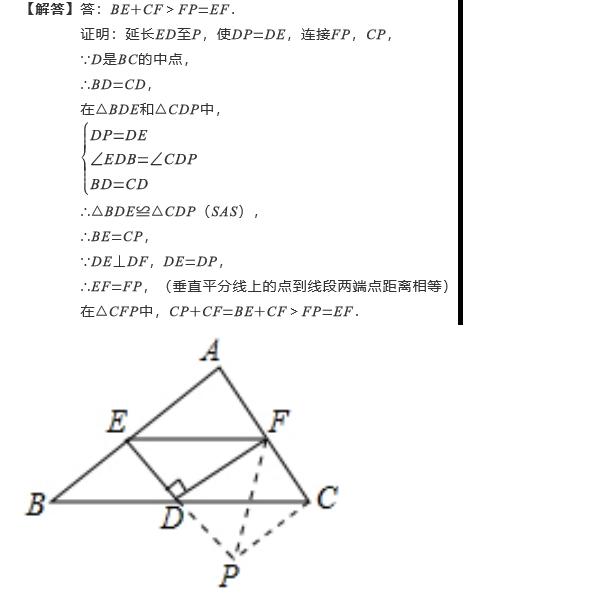

 加载中,请稍侯......
加载中,请稍侯......
精彩评论