八年级数学每日一练（9月23日-9月28日）含答案

【9月23日】图①、图②均是8×8的正方形网格，每个小正方形的顶点称为格点，线段OM、ON的端点均在格点上．在图①、图②给定的网格中以OM、ON为邻边各画一个四边形，使第四个顶点在格点上．要求：

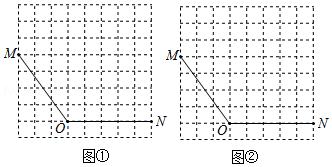
（1）所画的两个四边形均是轴对称图形．

（2）所画的两个四边形不全等．

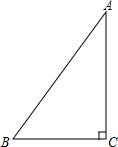
【9月24日】如图，△ABC中，∠C＝Rt∠，AB＝5cm，BC＝3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．

（1）出发2秒后，求△ABP的周长．

（2）问t满足什么条件时，△BCP为直角三角形？

（3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？

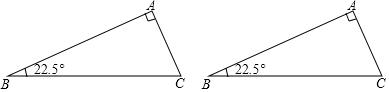
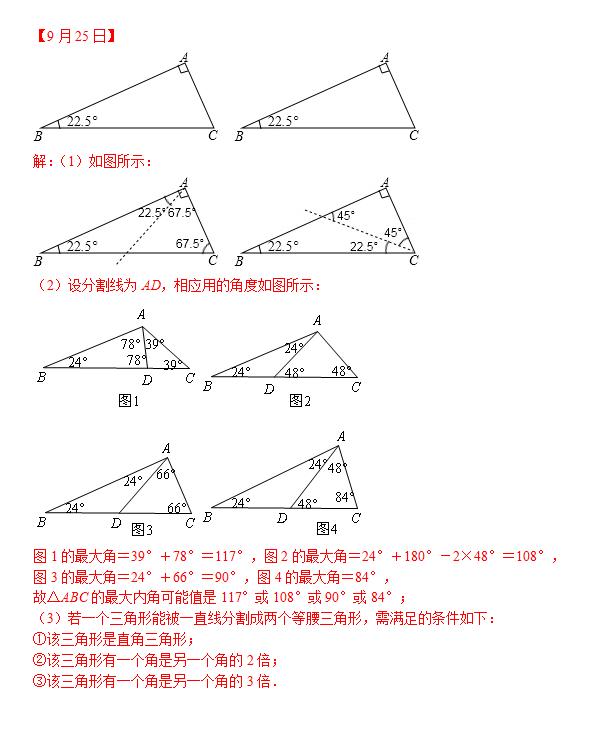
【9月25日】（1）操作实践：△ABC中，∠A＝90°，∠B＝22.5°，请画出一条直线把△ABC分割成两个等腰三角形，并标出分割成两个等腰三角形底角的度数；（要求用两种不同的分割方法）

（2）分类探究：△ABC中，最小内角∠B＝24°，若△ABC被一直线分割成两个等腰三角形，请画出相应示意图并写出△ABC最大内角的所有可能值；

（3）猜想发现：若一个三角形能被一直线分割成两个等腰三角形，需满足什么条件？（请你至少写出两个条件，无需证明）

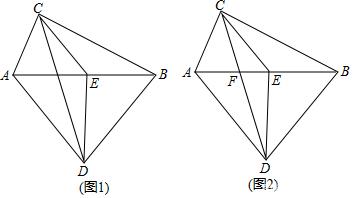
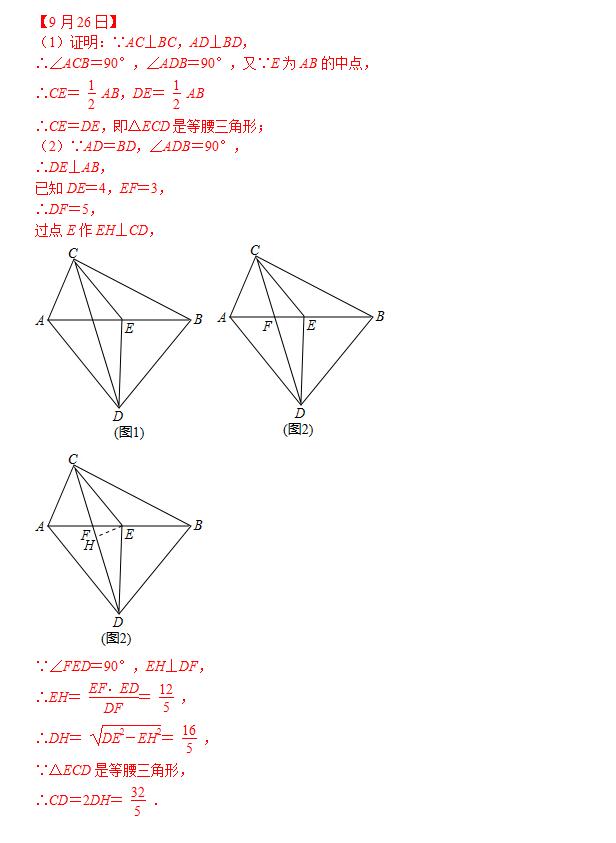
【9月26日】如图，已知AC⊥BC，AD⊥BD，E为AB的中点，

（1）如图1，求证：△ECD是等腰三角形；

（2）如图2，CD与AB交点为F，若AD＝BD，EF＝3，DE＝4，求CD的长．

【9月27日】如图，在Rt△ABC中，∠C＝90°，∠A＝30°．点D是AB中点，点E为边AC上一点，连接CD，DE，以DE为边在DE的左侧作等边三角形DEF，连接BF．

（1）△BCD的形状为_________；

（2）随着点E位置的变化，∠DBF的度数是否变化？并结合图说明你的理由；

（3）当点F落在边AC上时，若AC＝6，请直接写出DE的长．

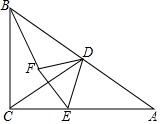
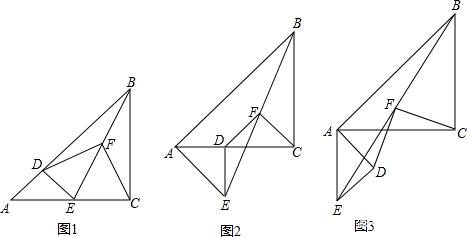
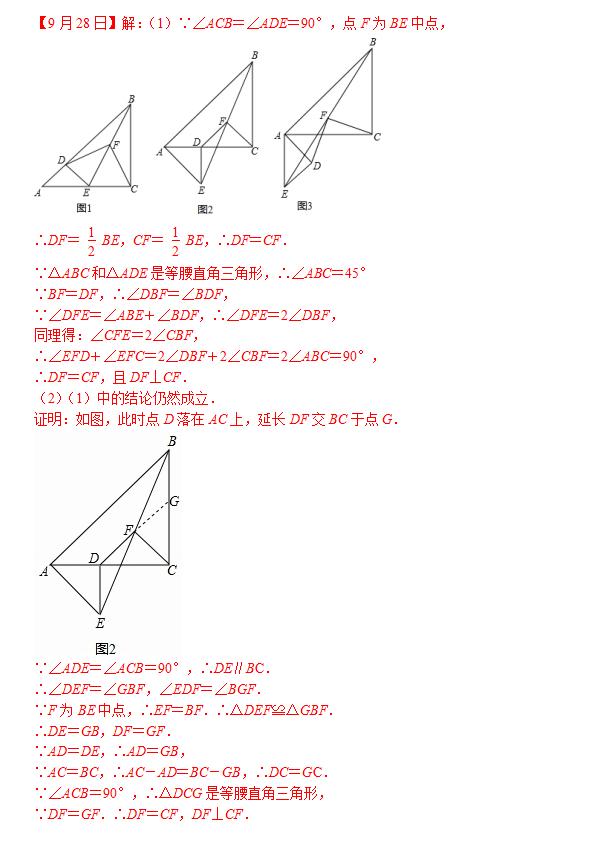
【9月28日】已知△ABC和△ADE是等腰直角三角形，∠ACB＝∠ADE＝90°，点F为BE中点，连接DF、CF．

（1）如图1，当点D在AB上，点E在AC上，请直接写出此时线段DF、CF的数量关系和位置关系（不用证明）；

（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；

（3）如图3，在（1）的条件下将△ADE绕点A顺时针旋转90°时，若AD＝1，，求此时线段CF的长（直接写出结果）．