相似三角形性质在解题中的应用

本文例说运用相似三角形性质解题

一、作辅助线，构造相似三角形

例1 （深圳）如图1，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD：BE的值为

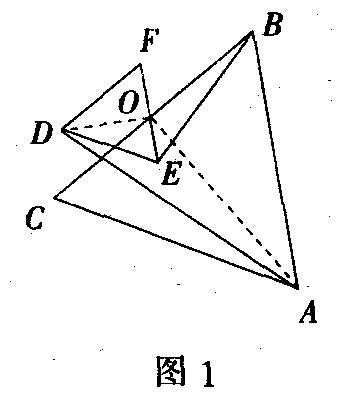
分析 由于点O是等边△ABC和等边△DEF的边BC、EF的中点，所以，联结OA，OD是常用的辅助线．有

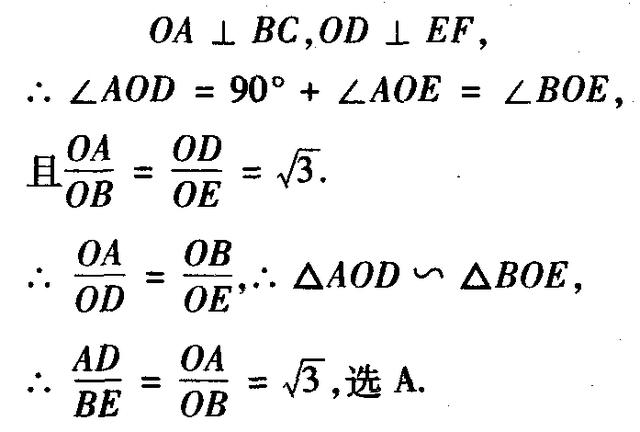
这里，我们利用相似三角形的性质，使未知和已知之间建立了桥梁作用．

二、利用矩形性质，找出相似三角形

例2 （山西）如图2，在平面直角坐标系中，矩形OABC的对角线AC平行于x轴，边OA与x轴正半轴的夹角为30°，OC＝2，则点B的坐标是_________．

分析 如图2，作BE⊥y轴于点E，BF⊥AC于点F设BC交y轴于点M，AC交y轴于点N，问题转化为求线段NF，BF的长．

这里，我们充分运用矩形的性质和坐标系的特点，利用相似三角形对应边成比例，使问题得以解决．

三、结合运用三角形中位线定理

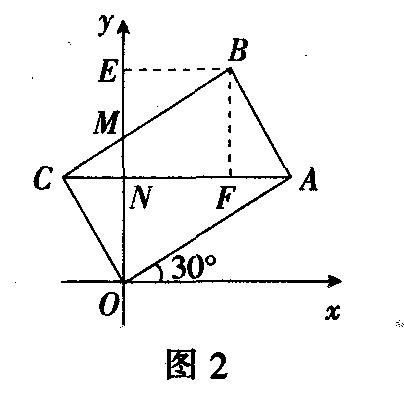
例3（安徽）如图3，在△ABC中，D、E、F分别为三边的中点，G点在边AB上，△BDG与四边形ACDG的周长相等，设BC＝a，AC＝b，AB＝c．

(1)求线段BG的长；

(2)求证：DG平分∠EDF；

(3)联结CG，若△BDG与△DFG相似，求证：BC⊥CG．

分析 (1)由于△BDC与四边形ACDG的周长相等，且BD＝DC，D、E、F分别为三边的中点，由图3知，

(3)∵△BDG与△DFG相似，并没有指明对应顶点，因此，我们要通过推理，说明它们的对应角是哪两个角．

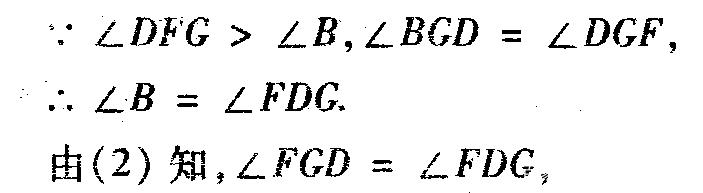
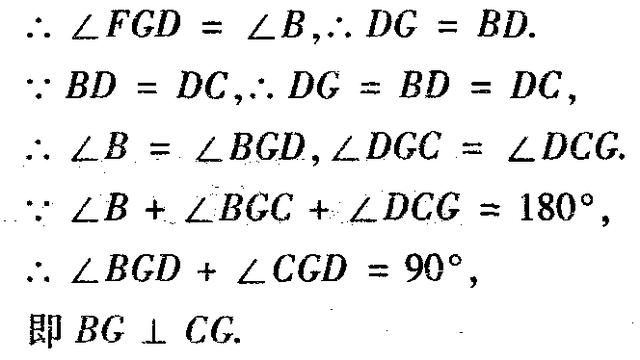
这里，我们综合应用了相似三角形的判定和性质，也体现了数形结合思想和整体思想，这是解几何综合题常用的方法．

四、结合运用分类讨论

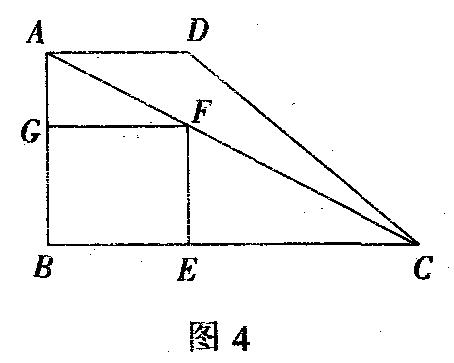
例4（重庆）已知：如图4，在直角梯形ABCD中，AD∥BC，∠B＝90°，AD＝2，BC＝6，AB＝3．E为BC边上一点，以BE为边作正方形BEFG，使正方形BEFG和梯形ABCD在BC的同侧．

(1)当正方形的顶点F恰好落在对角线AC上时，求BE的长；

(2)将(1)问中的正方形BEFC沿BC向右平移，记平移中的正方形BEFG为正方形B'EFG，当点E与点C重合时停止平移．设平移的距离为t，正方形B'EFC的边EF与AC交于点M，联结B'D，B'M，DM，是否存在这样的t，使△M'DM是直角三角形？若存在，求出t的值；若不存在，请说明理由；

(3)在(2)间的平移过程中，设正方形B'EFC与△ADC重叠部分的面积为S，请直接写出S与t之间的函数关系式以及自变量t的取值范围．

分析 (1)如图4，设正方形BEFG的边长为x，则BE＝FC＝BC＝x．

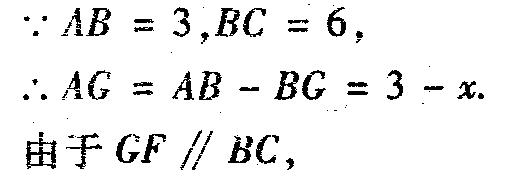
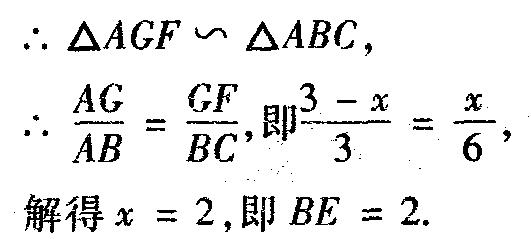
(2)假设存在满足条件的实数t．如图5，过点D作DH⊥BC于点H，则

BM＝AD＝2．DH＝AB＝3．

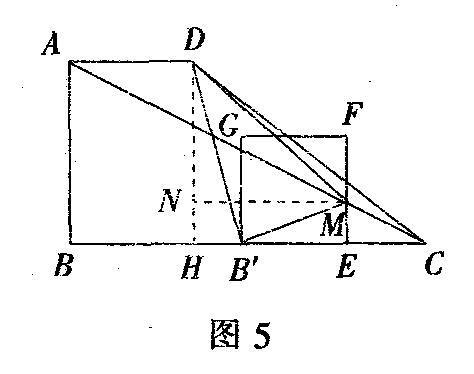
由于条件中仅给出△B'DM是直角三角形，并没有明确哪一个角是直角，所以，要考虑三个角都可能是直角，为此，要进行分类讨论．

题中，我们综合应用了平移的性质，相似三角形的判定和性质，勾殷定理，正方形的性质，直角梯形与函数的内容．