中考数学《二次函数》考点大通关

二次函数是初中数学的重要内容，也是中考必考的热点内容之一.下面就这部分内容的主要考点分类解析，希望能对读者有所帮助.

通关一:求二次函数的解析式

(一)利用定义求解

(二)利用一般式y=ax²+bx+c(a≠0)求解

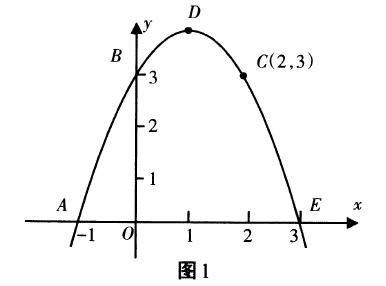
例2 如图1，在平面直角坐标系中，一抛物线经过A,B,C三点，且与x轴的另一个交点为点E，它的顶点为点D.

(1)求这个二次函数的解析式.

(2)求这个二次函数图象的顶点坐标.

(3)填空:把这个二次函数的图象沿坐标轴方向最少平移个单位长度，可使得该图象的顶点在原点.

(三)利用顶点式y=a(x-h)²+k(a≠0)求解

例3 在平面直角坐标系中，二次函数y=ax²+bx+c的图象的顶点坐标为(－2，－1),且过点(2,7)，求该二次函数的解析式.

(四)利用交点式y=a(x-x₁)(x-x₂)(a≠0)求解

例4 如图2，在平面直角坐标系中，一抛物线的顶点为点p(3,2)，且抛物线在x轴上截得的线段AB长为4个单位长度，求这个函数的解析式.

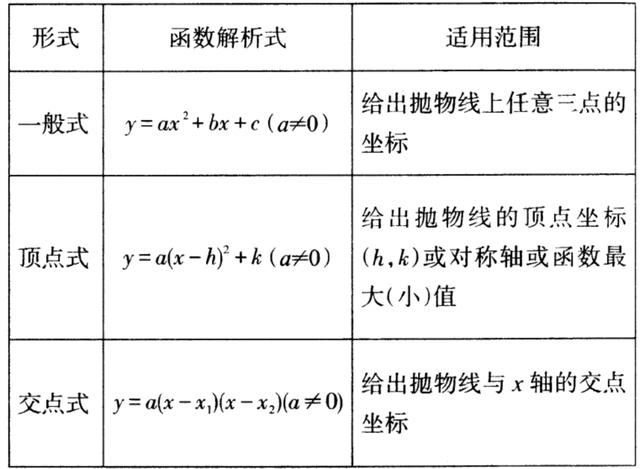
小结:求二次函数解析式的常用方法是待定系数法.当给定的条件不同时，所设的解析式也不一样，具体如下表所示:

通关二:二次函数的图象与系数的关系

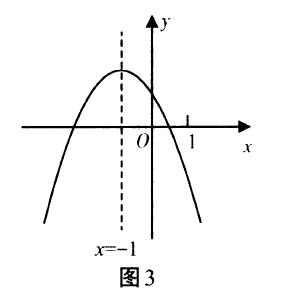
例5 在平面直角坐标系中，二次函数y=ax²+bx+c(a≠0)

的图象如图3所示，给出下列四个结论:①4ac-b²＜0,②4a+c＜2b,③3b+2c＜0,④m(am+b)+b＜a(m≠-1)，其中正确的结论有( ).

A.4个 B.3个

C.2个 D.1个

通关三:抛物线的平移、旋转和翻折

(一)由抛物线的平移来求新得二次函数的解析式

例6 在平面直角坐标系中，将二次函数y=-½x²+x+2/3的图象先向右平移2个单位长度，再向上平移6个单位长度，所得二次函数的解析式为______.

解析:本题应先将二次函数的解析式化为顶点式的形式，再根据平移规律确定平移后所得的函数解析式.

(二)由抛物线的旋转来求新得二次函数的解析式

例7 已知二次函数y=3x²-6x-5，在平面直角坐标系中，将其图象绕坐标原点顺时针旋转180º，求旋转后的函数解析式.

解析:根据旋转的特征可知，将抛物线绕原点旋转180º后，所得到的抛物线与原抛物线的形状相同，但开口方向变化了，顶点横、纵坐标是原抛物线顶点横、纵坐标的相反数.

(三)由抛物线的翻折来求新得二次函数的解析式

例8 在平面直角坐标系中，将二次函数y=2x²+4x-3的图象按下列要求进行翻折变换，求翻折后所得二次函数的解析式.

(1)沿y轴翻折.

(2)沿x轴翻折.

小结:在平面直角坐标系中，将二次函数的图象作平移、旋转或轴对称变换，有如下规律:

通关四:二次函数的图象和性质

例9 已知二次函数y=ax²+bx+c(其中a＞0,b＜0,c＜0)，关于这个二次函数的图象有如下说法:①开口一定向上;②顶点一定在第四象限;③与x轴的交点至少有一个在y轴的右侧.以上说法正确的个数为( ).

A .0 B .1

C.2 D.3

通关五:利用抛物线的对称轴解题

利用对称轴求解析式

例10在平面直角坐标系中，二次函数y=ax²+bx+c的图象的顶点坐标为(-1,4)，图象与

x轴两交点间的距离为6，求此二次函数的解析式.

小结:二次函数y=ax²+bx+c(a≠0)的图象是一条抛物线，对称轴是直线x=-a/2b，如果抛物线与x轴有两个交点的话，那么对称轴垂直平分两交点所连的线段，即两交点到对称轴的距离相等.

通关六:二次函数与一元二次方程的联系

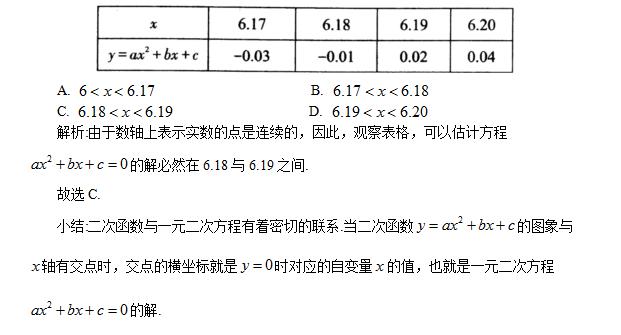
例13 下表是二次函数y=ax²+bx+c的自变量x与函数值y的对应值，判断方程ax²+bx+c=0

(a≠0，abc为常数)的一个解x的范围是( ).