距离公式的妙用——破解二次函数问题

等腰三角形问题和直角三角形问题是二次函数探究中常见的两类问题，如何快速正确地解决这两类问题，笔者在解题实践中发现，运用两点间距离公式，能起到较好的作用.

公式模型：在平面直角坐标系中，若A(x₁,y₁)，B(x₂,y₂).则A、B两点间的距离公式为

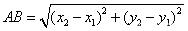
以下分类例说公式的运用.

一、等腰三角形类

例1如图1，已知二次函数的图像，经过原点和A(4,0)、B(3,3).P为二次函数的图像上的一个动点，过点P作X轴的垂线，垂足为M(m,0)，并与直线OB交于点C.

(1)求出二次函数的的表达式.

(2)当点P在直线OB上时，线段PC的最大长度是多少？

(3)当m＞0时，探索是否存在点P，使得△PCO为等腰三角形？如果存在，求出点P的坐标；如果不存在，请说明理由.

说明第1、2问较简单，略.下面只对第3问进行探究.

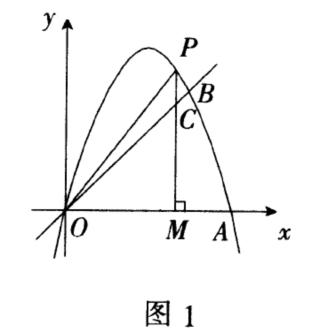
解 如图1，假设存在一点P，使得△PCO为等腰三角形，由(1)易得二次函数解析式为y=-x²+4x，直线OB的解析式为y=x，则P(m,-m²+4m)，C(m,m).

二、直角三角形类

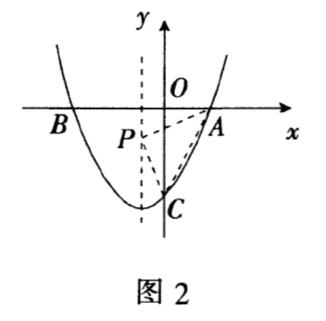
例2已知二次函数y=ax²+bx-2的图像，经过A(1,0)，B(-2,0)两点.

(1)求出二次函数的的表达式；

(2)在抛物线的对称轴上是否存在点P，使得△PAC为直角三角形？如果存在，求出所

有符合条件的点P坐标.

说明 第1问较简单，略.下面只对第2问进行探究.

三、解题反思

不论是等腰三角形，还是直角三角形，其核心要素是边，抓住了边，就抓住了问题的本质.而两点间距离公式提供了打通边的钥匙，根据边的关系，加以分类，建立方程，从而求得待定的数值.这种方法具有一般性，这正如张景中先生所说：“一种方法解很多题，要好过很多方法解一道题，这一种方法不是技巧性强，灵机一动的妙法，应是最基本，最重要，最自然的通法”.