深度剖析一类隐含圆的动点问题

挖掘隐含条件 破解动点问题

本文剖析一类隐含圆的动点问题，供同学们学习参考.

一、动点问题中可构建圆的基本结论

1.“定线定角”隐藏着外接圆

如图1，已知线段AB=4，点C是直线AB上方的一个动点，∠ACB=30°，动点C的路径是什么?

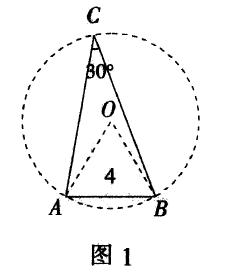
想一想:在直线AB上方找这样的点C，能找到多少个?把这些点连起来成的图形是怎样的图形?

通过思考可知，在直线AB上方可以找到无数个点C，把这些点连结起来是一条圆弧.

再想一想:如何画出弧所在的圆?

根据条件，圆周角是30°，圆心角是60°,画等边三角形△ABC就可以了. O点就是圆心，半径就是线段AB的长，可以画出一个圆.

实际上，这个问题可以这样理解:如图1,因为C点是动点，则A,B,C三点构成的△ABC是一个动三角形，其中线段AB是定长，∠是一个定角，且线段AB所对的角是∠.由“同圆或等圆中相等的圆周角所对的弦相等”可知，点C是在△ABC的外接圆上运动.画圆的关键是找圆心，定半径.因为AB是弦，⊙O的圆心是在AB的垂直平分线上，∠C是圆周角，所以在圆中所对的圆心角∠C是60°，即∠AOB=60°,OA=OB，画等边三角形△AOB，圆的半径R=4，动点C构成⊙O的一段优弧，即点C的路径长就是优弧ACB的长.

变式 其它条件不变，∠C的度数改为45°,60°,α (0°<α<90°)，求点C路径.

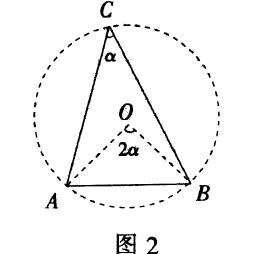
如图2，线段AB=4是定值，当∠C=α时，∠C=α的大小确定，即“定线定角”，根据“同圆或等圆中相等的圆周角所对的弦相等”，可知这些问题中所求C点应在某个圆上运动.构画出圆，从而使问题中原本隐含的条件和信息在圆中展现出来.

2.“公共料边的直角三角形”隐藏着外接圆

如图3，已知线段AB=4，画出平面内满足∠ACB=90°的所有动点C组成的图形.

想一想，能画出的是什么图形?

经过分析思考可知，所有动点C组成的图形是圆(图4).

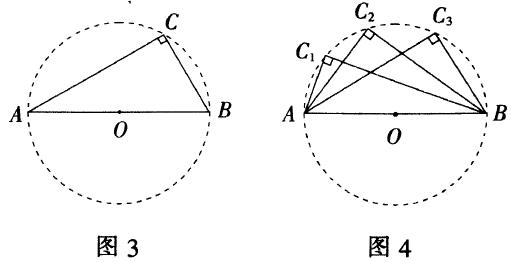
再想一想:

圆心怎么找?半径是多少?⊙O各点都是使∠ACB=90°的点C吗?

通过画图可让我们联想到:直径所对的圆周角是90°直角，从而画出隐藏的圆.

再根据“90°的圆周角所对的弦是直径”可知，AB是圆的直径，圆心是AB的中点，所以半径是2.点C在点A、点B处不能构成直角三角形，所以动点C组成的图形是除A,B两点的圆.

二、实际应用

例1 如图5，在平面直角坐标系中，点O为坐标原点，A,B,C三点的坐标分别为(√3,0),(3√3,0),(0,5)，且∠ADB=60°，点D在第一象限.求线段CD的最小值.

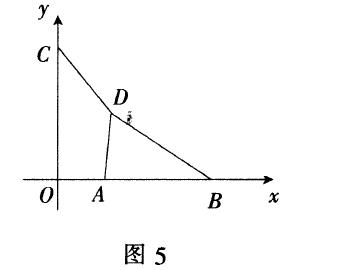
注：这道题中∠ADB=60°是定角，线段AB=2√3是定线段，由基本结论可知，存在一个隐圆，圆的半径是定值，求最值的问题就转化成圆外一点到圆上一点的最值问题.

例2 如图7，正方形ABCD的边长为2,P是对角线BD上的一个动点(不与B,D重合)，连结AP，过点B作BH⊥AP,H为垂足，连结DH，求线段DH的最小值.

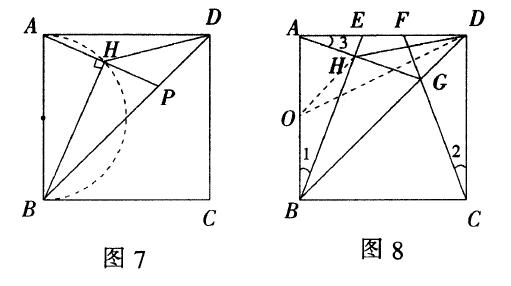
注：解题的关键是找到共斜边的直角三角形隐藏的外接圆.解题中要能自己创造图形，挖掘问题本质，就能知其然，也知其所以然，从而牢固建立系统的知识体系，而且能灵活应用所学的知识解决问题.

三、反思

1.认真审题 找突破口

近几年的中考试卷中常会出现动点问题，其中一类动点题，看似无圆，但其中隐藏着圆的模型.如“定线定角”、“有公共斜边的直角三角形”等.我们应通过去伪成真，让“圆”形显露，再利用圆的性质解决问题.

2.抓准延伸点 思维持续生长

在审题时要寻找题目中的特征，挖掘隐含条件，抓准知识的延伸点，让自己的思维持续生长.平时要注意积累解题方法，它对你来说就是一种解题模式，当你碰到类似问题或求解其他问题时，就能起到指引作用.解题后要归纳、总结和反思，使思维品质不断提升.

3.找出数学模型 求出正确结果

在平时的学习中，对基础知识、基本图形、基本方法、基本结论要进行深人研究，把解题的过程当作建立数学模型的过程，并在建模过程中培养自己的数学应用能力.变与不”都是相对的，变的是几何问题或图形，不变的是解题思路和数学本质.在解题过程中，要抓住图形的特点，从中发现解决该问题的数学模型，并快速求出正确结果.