一、试题呈现:平淡无奇道本质
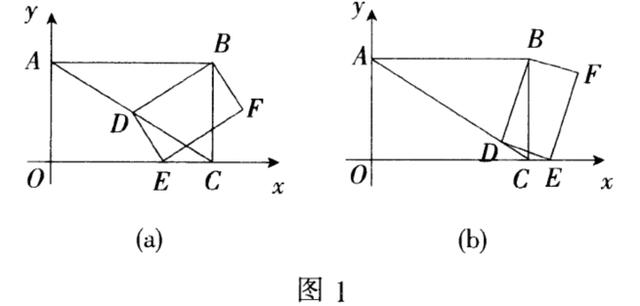
试题 (2017年广东中考题)如图1,在平面直角坐标系中,o为原点,四边形ABCD是矩形,点A,C
的坐标分别是A(0,2)和C(2√3,0),点D是对角线AC上一动点(不与A,C重合).连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
(1)填空:点B的坐标为_______.
(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由.
(3)①求证:DE/DB=√3/3;
②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.
2017年广东省中考压轴题的设计,一如既往地以动态变化类为基架,呈现方式自然朴实,淡化了压轴题的复杂计算,考查层次分明,不同水平的学生可以充分展示自己不同的探究深度.着重考查了三角函数、勾股定理的应用、二次函数求最值和代数综合运算等初中数学的核心内容,较好地体现了中考数学压轴题的选拔功能.
二、试题特色:关注学生,设问递进立意高
虽然是压轴题,但注重人性化,起点低,人口宽,不同层次的学生都能得到相应的分数.
第(1)问的问题情境熟悉,注重基础性的考查,关爱基础较差的学生,使他们也有展示的机会,体现人文性;
第(2)问考查了对分类讨论思想.运动类问题中,多数都以考查分类讨论思想方法为目的,而研究某个三角形变化的形状,可谓是这类问题的一种常规而经典的设计方式.比如这里,研究△DEC为等腰三角形,除了确定哪两条边相等,还需要讨论被动点E会出现边OC上,或OC的延长线上的两种情况.当点E在边OC上(如图1(a))时,易知DC=EC,∠EDC=∠ECD=30°,△DBC为等边三角形,从而得到∠DAB=∠DBA=30°,所以AD=BD=BC=2;当点E在OC的延长线上(如图1(b))时,易知DC=EC,∠CED=∠CDE=15°,∠ABD=∠ADB=75°,因此AD=AB=2√3.这里考查了学生的基本技能和基本思想.
第(2)问递进到第(3)问,称得上独具匠心,关注优等生的能力发展.这样的设问注意到了能力层次的要求和问题间的关联,较好地体现了中考数学压轴题的选拔功能.
三、试题分析:注重基本“套路”,突出数学思想
1.重视基本图形
解决几何问题的一个基本套路,首先要认真分析条件,将条件与相关“基本图形”结合起来,利用这个“基本图形”的性质,获得相应的结论.有时图形中不一定有与条件匹配的“基本图形”,这时还需要联想相关知识作辅助线构造出相关的“基本图形”;再利用这个“基本图形”的性质,获得相应的结论,达到解决问题的目的.
对于第(3)问①的证明,容易得到:
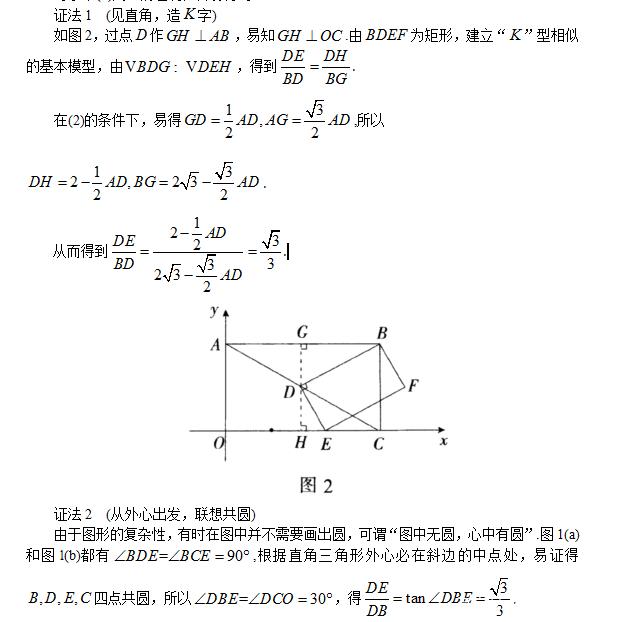
评注几何综合题的图形中往往隐去了基本图形的一部分,如果能联想到相应的基本图形,并能适时发现和添出辅助线(辅助圆),再现基本图形,解题思路就会柳暗花明.可以这样说,一种辅助线作法对应着一个基本图形,辅助线就是把残缺的基本图形补充完整,从而利用基本结论解题
2.突出数学思想
本题并非是解题方法和技巧的机械运用,而是巧妙考查了学生的化归思想、建模思想、分类思想、方程与函数思想等,强化了对数学理性思维的能力要求,展现了数学的学科价值和人文价值.
(1)分类讨论思想
第(2)问思路容易形成,第一次分类讨论,需要确定△DEC中谁是顶点.第二次分类讨论,需要讨论主动点D在对角线AC上运动时,被动点E在x轴上,会出现边OC上,或在OC的延长线上的两种情况.
(2)建模思想
第(3)问①的证明:无论是建立“K”型相似的基本模型,或是证明B,D,E,C四点共圆的解决办法,都是在提炼基本模型,以模解题,打破思维定势,化陌生为熟悉,化非常规为常规.这将有助于学生体验数学基本经验在解决实际问题中的价值和作用,强化应用意识.
(3)方程与函数思想
二次函数是初中代数的核心内容,历来都是中考必不可少的一项内容.解第(3)问②通过面积问题,灵活使用方程与函数知识,表现出本题的命题的基础性、实用性和教学的导向性.
近年中考中特别重视突出数学思想方法的考查.因此,在平时的教学中,要注意体会、归纳教材、题目中的数学思想方法.尤其在中考复习时,教师更应有意识、有目的、适时地渗透数学思想方法,培养学生有效利用数学思想方法解决相关问题的能力.

 加载中,请稍侯......
加载中,请稍侯......
精彩评论