一道二次函数题有十种解法？总有一种适合你

苏东坡的《题西林壁》的“横看成林侧成峰，远近高低各不同”中横看、侧看、远看、近看给我们形象的展示了一题多解的精髓.一题多解可以开阔学生思路，发散学生思维，加深学生的思维深度，可以培养思维的独创性，培养思维的变通性.从心理学角度讲，发散思维和集中思维的有机结合，正是培养创造性思维的有效途径.

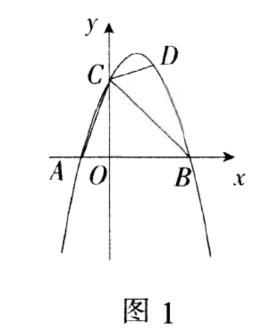
例题 已知如图1，二次函数y=-x²+2x+3交x轴于A,B两点，与y轴交于C点，若∠ACB=∠BCD时，求点D的坐标.

思维一 直接使用角相等条件

解题思考1:直接用∠ACB=∠BCD

①构造全等

在∠ACB=∠BCD，BC=BC的前提下，

(1)取∠CBE=45°，E在CD的延长线上，利用“ASA”构造全等.

(2)取CA=CE，利用SAS构造全等.

易得E(3,4)再用待定系数法求得直线CE的解析式最后用函数交点的意义求解D的坐标.

解法一：

②构造相似

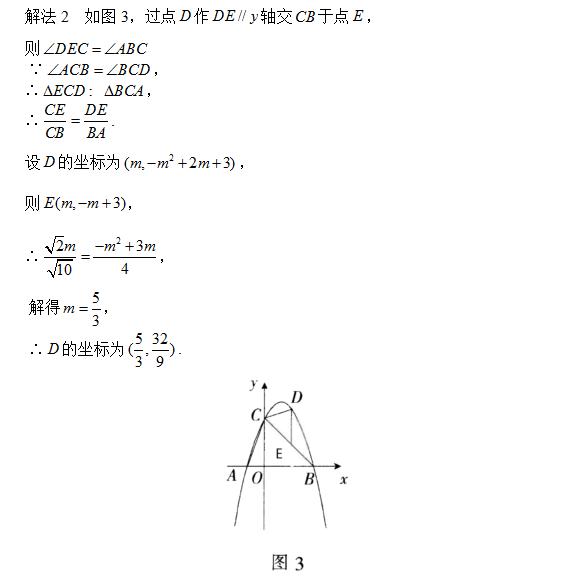
在∠ACB=∠BCD的前提下，取∠DEC=∠ABC(或作直线BE∥y轴也可得).

构造⊿ECD:⊿BCA再利用相似三角形的对应边成比例的性质建立方程求解点D的坐标.

解法二

③利用角平分线的定义，“图中有角平分线，可以将图形对着看，对称以后关系显现.” 将∠ACB沿BC翻折，A的对应点A₁，且A₁在CD延长线上，再利用对称中的知识:H为AA₁的中点和Kbc·Kaa₁=-1求解A₁的坐标.进而求得点D的坐标或利用中垂线定理可得AB=AA₁同①可求得点D的坐标.

解法三

④利用tan∠BCD=tan(∠ACO+∠OCB)=2

再利用tan∠BCD=2，构造Rt⊿BCH，再作K型相似模型.

(1)过点B作BE⊥BC交CD的延长线于点E;

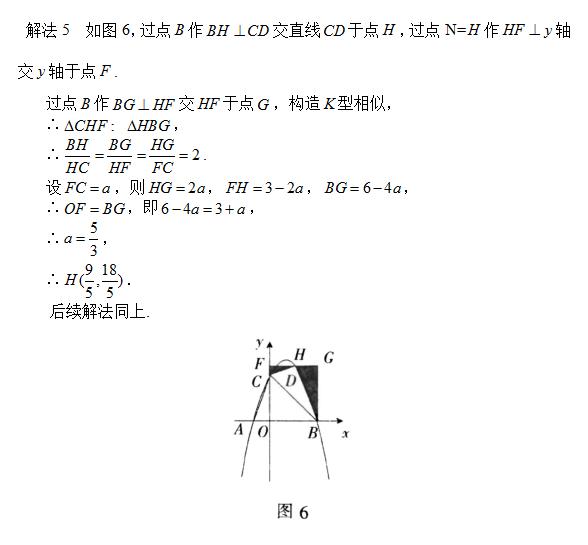
(2)过点B作BH⊥CD交直线CD于点H.

解法四

解法五

思维二 间接使用角相等条件

∠ACB=∠BCD→∠ACO+45°→∠DCF+45°→∠ACO=∠BCD.

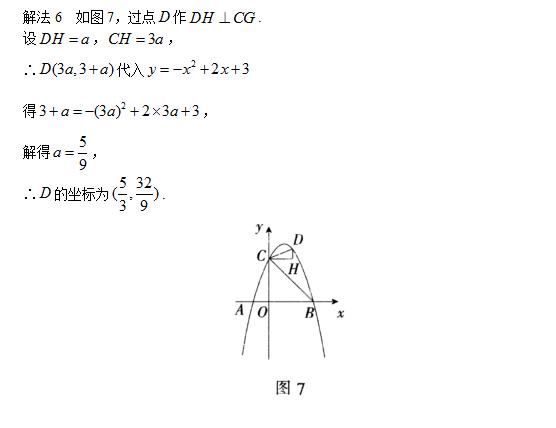
解法六

解法七

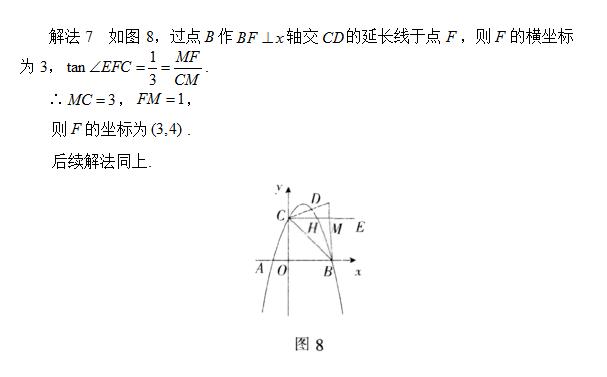
小结 发现要求点D的坐标可先求CD的直线解析，求解析式的思路拓展:

(1)求k和b，k=tanθ=tan∠DCE(θ为直线与x轴的夹角);

(2)两点确定一条直线(C为已知点，可求另一点，最简单点即为与x轴的交点).

解法八

设CD的直线解析式为:y=kx+b(k≠0).

由一次函数的几何意义可知k=3，b=3，后续解法同上.

解法九

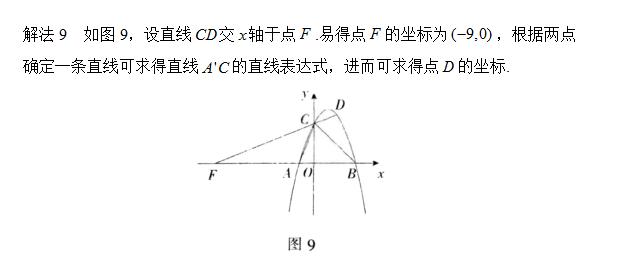
思维三用条件构造模型

利用角平分线、平行线、等腰三角形的“知识板块”思维.角平分线、平行线、等腰三角形若见其一，应思其二，想其三;或作其二，寻找发现其三，这种解题思路方法往往能得到打开第一道大门的金钥匙，突破解题的一个难点，使一类题目变难为易成为可能.

解法十