巧妙设元求解行程问题，学会再也不怕

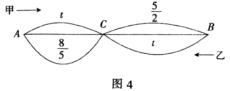
例1：甲、乙两车同时分别从A、B两站相对开出，在A、B两站之间不断往返行驶，甲、乙两车的速度分别是15千米/小时、35千米/小时，并且甲、乙两车第三次相遇地点与第四次相遇地点恰好相距100千米，求A、B两地的距离.

分析1 甲、乙两车速度比为3：7.第一次相遇时甲、乙两车所走路程的比为3: 7，将A、B两站的路程十等分，可知第一次相遇点在C处，第二次相遇点在D处，第三次相遇点在E处，第四次相遇点在F处.

分析2 甲、乙第三次相遇所走路程的和是A、B两站间的距离的5倍，即甲第三次相遇所走总路程是甲第一次相遇时所走路程的5倍.甲、乙第四次相遇所走路程的和是A、B两站间的距离的7倍，即甲第四次相遇所走总路程是甲第一次相遇时所走路程的7倍.

略解 设第一次相遇时甲、乙所走路程分别为3a千米、7a千米，从而得出第三次相遇点距A

为（20a-5*3a）=5a，第四次相遇点距A为(7*3a-2*10a)=a，可列方程

5a-a=100,∴a=25

∴10a=250km.

例2 ：在边防沙漠地带，巡逻车每天行驶200公里，每辆巡逻车可装载供行驶14天的汽油.现有5辆巡逻车同时从驻地A出发，完成任务后再沿原路返回.为了让其中3辆车尽可能向更远的距离巡逻(然后一起返回)，甲、乙两车行至途中B处后，仅留足自己返回驻地所必须的汽油，将多余的汽油留给另外3辆使用.问其它3辆车最远能行驶多远的距离？

分析 为了让其中3辆车尽可能向更远的距离巡逻，须使3辆车在B处的存油量最多(即为装满时).即是甲、乙两车向3辆车所提供的油量等于这3辆车在AB段的耗油量.

略解：设每辆汽车在AB段耗油量为x天汽油量，可列方程

2(14-2x)=3x,∴x=4

∴最远距离为S=（14-4）÷2×200+4×200=1800km

变题 若将原题中甲、乙两车行至途中B处后，留足5辆车返回驻地所必须的汽油，将多余的汽油留给另外3辆使用.问其它3辆车最远能行驶多远的距离？

分析 为了让其中3辆车尽可能向更远的距离巡逻，须使3辆车在B处的存油量最多(即为装满时).即是甲、乙两车向3辆车所提供的油量等于这3辆车在AB段往返的耗油量.

略解：设每辆汽车在AB段耗油量为x天汽油量，可列方程

2（14-2x）=2*3x，∴x=2.8

∴最远距离S=14÷2×200+2.8×200=1960km

例3：一个人骑自行车从A地至B地，3小时到达B地，同时，另一个人骑自行车从C地出发，要使他们同时到达B得，后者每走1公里少用1分钟，由C到B地的距离比A到B地的距离多6公里，求这两段距离.

例4：公共汽车每隔一定时间发一趟车，小宏在街上行走，发现从背后每隔6分钟开过一辆公共汽车，而每隔30/7分钟迎面开来一辆公共汽车.如果公共汽车与小宏行进的速度都是均匀的，求车站每隔多少分钟发一趟车.

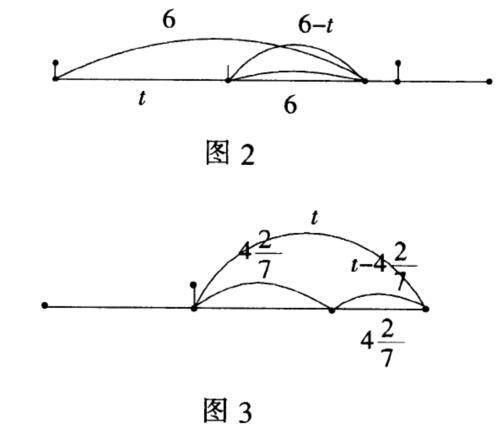
分析 相同距离内(即距离一定)，两次的时间的比都等于速度的反比.

例5：某停车场内有10辆出租汽车，第一辆出租汽车出发后，每隔4分钟开出一辆出租汽车.在第一辆出租汽车开出2分钟后，有一辆出租汽车回场，以后每隔6分钟有一辆出租汽车回场，回场的出租汽车依次排队，每隔4分钟开出一辆，问经过多少时间停车场第一次没有出租汽车？

分析 在第8分钟时，开出3辆车进场2辆车，停车场剩下9辆车，以后每隔12分钟，停车场减少1辆车，到第7个12分钟，停车场剩下2辆车，第8个12分钟停车场出现开出最后一辆车的同时有一辆车准备即将开进(8+8×12= 104分钟).由此，停车场没有出租汽车，可以看成停车场开出最后一辆车的同时有一辆车准备即将开进，满足这个条件须使所有开出汽车的总时间不大于场外开进汽车的总时间.

略解 设停车场内共有x辆次出租汽车停靠，则此时停车场外有（x-10）辆次出租汽车则，可列不等式4（x-1）≤6(x-10)+2，∴x≥27.

因x取最小正整数，∴x=27, ∴经过时间=4(27-1)=104分钟.

例6 ：A、B两地间的路程为36公里，甲从A地，乙从B地同时出发相向而行，两人相遇后，甲走2小时30分到达B地，乙再走1小时36分到达A地，求两人的速度.

解决数学问题，常常能碰撞出思维的火花，有时稍纵即逝，需要及时的捕捉.笔者在多年教学和揣摩的基础上，经过精心整理和筛选，提供给读者，以利于教学相长.