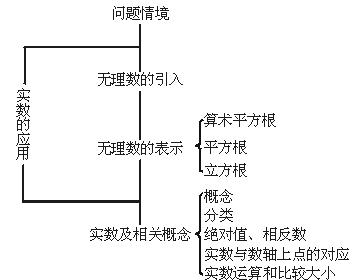
数的开方主要知识点及例题:
1【平方根】:
1.如果一个数x的平方等于a,那么,这个数x就叫做a的平方根;也即,当x²=a(a≥0)时,我们称x是a的平方根,记做:x=±根号a。
2.当a=0时,它的平方根只有一个,也就是0本身;
3.当a>0时,也就是a为正数时,它有两个平方根,且它们是互为相反数,通常记做:x=±根号a。当a<0时,也即a为负数时,它不存在平方根。

2【算术平方根】:
1.如果一个正数x的平方等于a,即x²=a,那么,这个正数x就叫做a的算术平方根,记为:“根号a”,读作,“根号a”,其中,a称为被开方数。特别规定:0的算术平方根仍然为0。
2.算术平方根的性质:具有双重非负性,即:根号a≥0(a≥0)。
3.算术平方根与平方根的关系:算术平方根是平方根中正的一个值,它与它的相反数共同构成了平方根。因此,算术平方根只有一个值,并且是非负数,它只表示为:根号a;而平方根具有两个互为相反数的值,表示为:±根号a。

3【立方根】
1.如果x的立方等于a,那么,就称x是a的立方根,或者三次方根。记做:三次根号a,读作,3次根号a。注意:这里的3表示的是开根的次数。一般的,平方根可以省写根的次数,但是,当根的次数在两次以上的时候,则不能省略。
2.平方根与立方根:每个数都有立方根,并且一个数只有一个立方根;但是,并不是每个数都有平方根,只有非负数才能有平方根。

4【无理数】
1.无限不循环小数的小数叫做无理数;它必须满足“无限”以及“不循环”这两个条件。
2. 有理数与无理数的区别:(1)有理数指的是有限小数和无限循环小数,而无理数则是无限不循环小数;(2)所有的有理数都能写成分数的形式(整数可以看成是分母为1的分数),而无理数则不能写成分数形式。

5【实数】
1.有理数与无理数统称为实数。在史书中,没有最大的实数,也没有最小的实数;绝对值最小的实数是0,最大的负整数是-1。
2.实数的性质:实数a的相反数是-a;实数a的倒数是a分之一(a≠0);实数a的绝对值|a|=a(a≥0),|a|=,-a(a≤0),它的几何意义是:在数轴上的点到原点的距离。
3.实数的大小比较法则:实数的大小比较的法则跟有理数的大小比较法则相同:即正数大于0,0大于负数;正数大于负数;两个正数,绝对值大的就大,两个负数,绝对值大的反而小。(在数轴上,右边的数总是大于左边的数)。对于一些带根号的无理数,我们可以通过比较它们的平方或者立方的大小。
4.实数的运算:在实数范围内,可以进行加、减、乘、除、乘方、开方六种运算。运算法则和运算顺序与有理数的一致。


 加载中,请稍侯......
加载中,请稍侯......
精彩评论