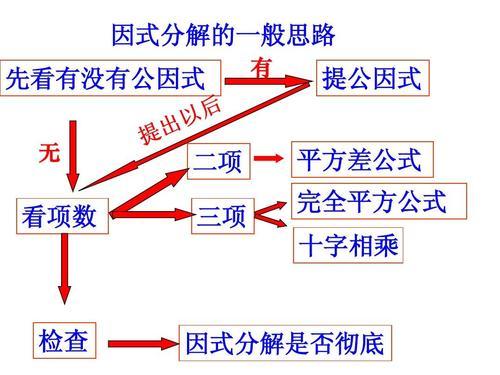
不少同学在学习了因式分解的基本方法后,解题时还会遇到这样那样的一些小问题,而造成分解的思路不畅,或者分解不彻底.为了帮助同学们解决这些小问题,在此介绍几种因式分解的“小招数”,希望对同学们有所帮助.
一、符号变一变
例1 分解因式-a²+2-1.
解 原式=-(a²-2a+1)=-(a-1)²
评析 原式有三项,虽有完全平方的“形”却不能直接用公式,提取“一”号后,便能套用“完全平方公式”.
二、位置动一动
例2 分解因式-4b²+a².
解 原式=a²-4b²=a²-(2b)²=(a+2b)(a-2b)
评析 原式是两项式,无公因式可提,需将两项位置对调,才能化为“平方差公式”的形式.
三、系数提一提
例3 分解因式:-¼a²+a-1
解 原式=-¼(a²-4a+4)=-¼(a-2)²
评析 原式有三项,提取首项的系数-¼后,括号内的因式便可套用“完全平方公式”分解.
四、括号添一添
例5 分解因式:a²(a-1)-a+1.
解 原式=a²(a-1)-(a-1)
=(a-1)(a²-1)
=(a-1)(a+1)(a-1)
=(a-1)²(a+1).
评析 如果把原式不问青红皂白,直接去括号,便弄得越来越复杂,仔细观察原式特点,把
-a+1添“一”括号,整个式子中便出现了公因式(a-1),下面的分解就容易了.
例6 分解因式4a²-9b².
解 原式=(2a)²-(3b)²
=(2a+3b)(2a-3b).
评析 如果把原式直接套用“平方差公式” ,将出现错误的结果:(4a+9b)(4a-9b),添括号后整理成“平方差公式”的形式,便可以正确分解了.
例7 分解因式4a²+12ab+9b².
解 原式=(2a)²+12ab+(3b)²=(2a+3b)² 评析 如果把原式直接套用“完全平方公式” ,将出现错误的结果:(4a+9b)²
显而易见,文中提到的几种“小招数” ,在同学们的解题过程中经常会用到,这几种“小招数”的实质,是把比较乱的多项式整理成为我们熟悉的便于用“公式法”或用“提取公因式法”来分解的形式,从而达到化难为易、化繁为简的目的.“招数”虽小你可不要小觑,只有熟练掌握这些“小招数” ,你在解决因式分解问题时才能得心应手、顺风顺水!

 加载中,请稍侯......
加载中,请稍侯......
精彩评论