七上数学：绝对值化简问题的归类分析2

接《绝对值化简问题的归类分析1》

六、已知不等式组的解集，变形二次根式后再化简绝对值

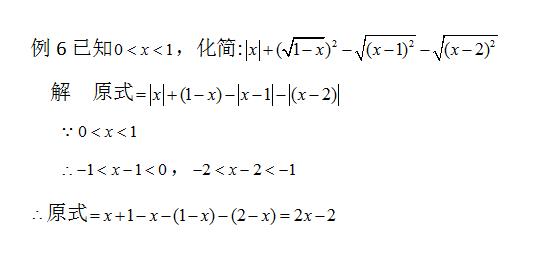
分析 本题涉及到了二次根式的性质（根号a）=a，根号a²=∣a∣的运用.解答时先将二次根式变形，进行第一次化简，再根据不等式的性质确定绝对值内的式子的符号，最后就可以化简绝对值.

七、解不等式组，再变形二次根式化简绝对值

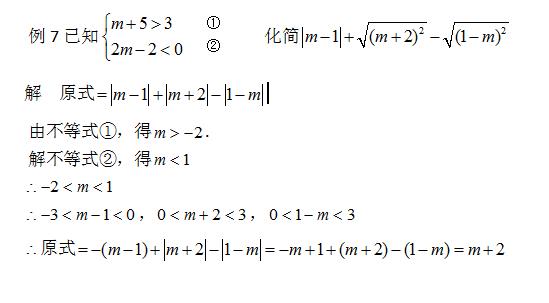
分析 ：本题涉及了一元一次不等式组的解法，二次根式的性质（根号a²=∣a∣）的运用.解答时，先求出m的解集，再将二次根式转化为绝对值，由不等式的性质确定绝对值内的代数式的符号，就可以由绝对值的性质化简.

八、由方程组的解建立不等式组，求出解集，再化简绝对值

分析 ：要去掉绝对值，得知道a的解集.必须先求出二元一次方程组的解，由二元一次方程组的解建立不等式组，求出a的解集，最后根据不等式的性质结合零点分段法分类讨论，确定a-3，a+1的符号，就可以化简绝对值.

九、由二次根式性质求不等式的解集，根据二次根式的性质变形为绝对值，再化简

分析 ：要解答此题，最终还是要化简绝对值.先根据二次根式的性质求出y的解集;再将（根号下y²-8y+16）的被开方数写成完全平方公式的形式，由二次根式的性质（根号a²=∣a∣）将二次根式转化为绝对值;最后由不等式的性质确定绝对值里面的式子的符号即可.

十、由二次根式的性质建立不等式组求出解集，再变形为绝对值化简

分析 ：要化简此题，需要运用二次根式的性质（根号a²=∣a∣）变形，再运用隐含条件1-x≥0，x＋2≥0建立不等式组求出x的解集，并运用完全平方公式将二次根式变形后转化为绝对值.最后由不等式的性质判断绝对值里面的式子的符号，就可以去掉绝对值符号，进而达到化简目的.

综上，绝对值的化简问题一般与不等式或不等式组、二次根式等综合在一起，以增加化简的难度.但是无论怎样情形，万变不离其宗，只要大家熟练掌握不等式的性质、二次根式的性质和绝对值的性质，灵活运用这些性质进行变形、化简，确定绝对值内的代数式的符号，那么绝对值化简的问题也不难.