巧用图形的轴对称性解题

∠ACD=∠BCD如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴，我们也说这个图形关于这条直线轴对称.巧妙利用图形的轴对称性解决问题，往往能达到事半功倍的效果.

例1 (2002年河南省初二数学竞赛试题)如图1,D为等边三角形ABC内一点，DB=DA,BF=AB,∠DBF=∠DBC，求∠BFD的度数.

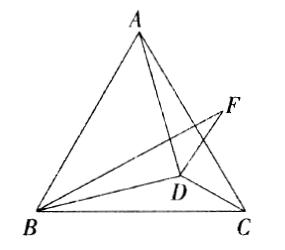
简析 由AC=BC,BD=AD可知，点A和点B关于直线CD对称，又根据轴对称的性质，可得∠ACD=∠BCD.

∵∠ACB=60° ,∴∠ACD=∠BCD=30°.

由BF=AB,AB=BC，得BF=BC.

又∵∠DBF=∠DBC.

∴⊿BFD与⊿BCD关于直线BD对称，

∴∠BFD=∠BCD=30° .

点评 此题若直接求解可以说很困难，然而合理利用题目的条件，用了两次轴对称，问题便迎刃而解.

例2 (1992年四川省数学竞赛题)如图2，正方形ABCD中，E是AD边的中点，BD与CE相交于点

F，求证:AF⊥BE.

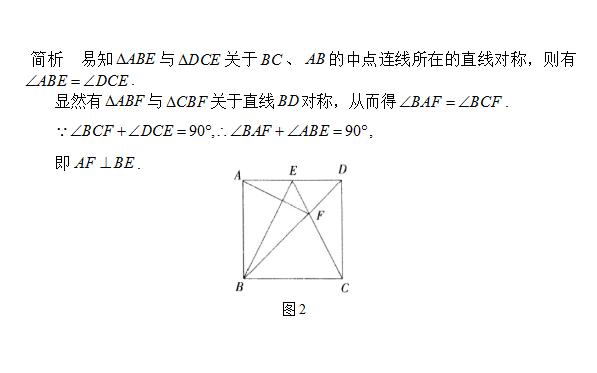
点评 本题从证明∠BAF+∠BAE入手，充分运用正方形的轴对称性，通过两次轴对称把两个角合理转化，使整个问题一目了然.

例3 (2003年湖北省黄冈市初中数学竟赛题)如图3，在⊿ABC中，AD是∠BAC的外角平分线，P是AD上异于点A的任意一点，试比较PB+PC与AB+AC的大小，并说明理由.

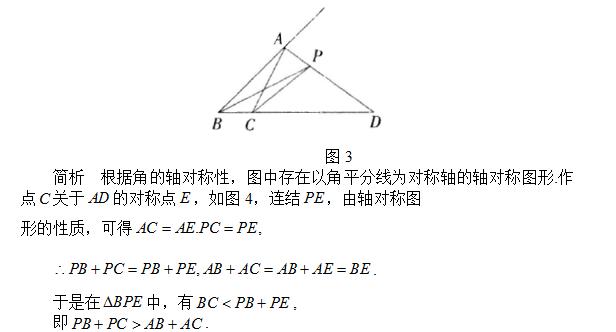
点评 本题运用轴对称把分散的条件转化到同一三角形中，根据三角形三边关系，使问题轻松得以解决.

以上三例充分说明，合理利用图形的轴对称性解题，常可以使复杂问题简单化.