例谈平行线上两动点之间距离最短问题

初中几何中有一类关于距离最短的问题，这些问题最终都会转化为“垂线段最短”或“两点之间线段最短”.本文就一类平行线上两动点之间距离最短问题，谈谈笔者对此的分析和见解，以供读者参考.

PM+PN最小值这类题目解题步骤总结：①将点P,点M，点N分为动点与定点

②找到动点的运动轨迹

③将定点沿着动点的运动轨迹翻折得到定点的对称点

④将对称点与另一个定点连接起来，这个距离就是最短距离

一、基本问题

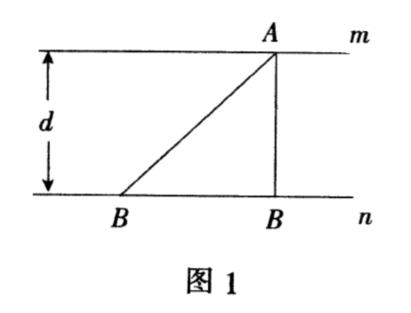
如图1，直线m∥n，且两直线之间的距离为d，若点A和点B分别是直线m，n上的动点，则点A和点B之间的距离最小值为d.

解析： 根据运动的相对性，不妨固定点A，则问题就变成了直线n外有一定点A到直线n上一动点B的距离最短问题.根据“垂线段最短”可知，当AB⊥直线n时，线段AB最短，此时，点A

和点B之间的距离最小值即为直线m和直线n之间的距离，即d.

二、应用

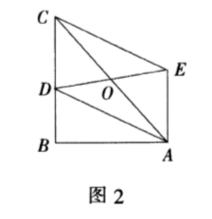
例1 如图2，在RT⊿ABC中，∠B=90°,AB=4,BC＞AB，点D在BC边上，在以AC

为对角线的平行四边形ADCE中，试求DE长的最小值.

解析 由四边形ADCE为平行四功形可知，AE∥BC，且两平行线间的距离为AB的长，即点D

和点E可看作两平行线上的各一动点，因此，当DE垂直于BC时，DE的长取得最小值，其最小值为4.

例2 如图3，在RT⊿ABC中，∠C=90°，AB=4,点F是线段AC上一点，经过点A的⊙F交

AB于点D，且ED=EB，求EF的最小值.

例3 :如图4，在四边形ABCD中，AD∥BC,AB⊥BC,AD=1,BC=3.点P是AB边上的一个动点，连接PD并延长至点E，使得PD:PE=1:3，以PE,PC为边作平行四边形PEFC，连PF，试求PF长的最小值.

例4: 如图5，在等边三角形ABC中，AB=4,点P,M,N分别是BC,AC,AB边上的动点，试求

PM+PN的最小值.

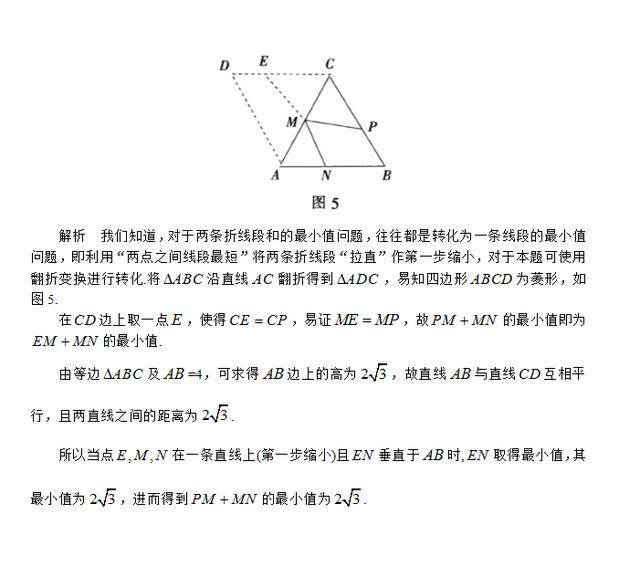
不难看出，例1是基本问题的直接应用;例2和例3是通过作垂线将两个动点置于两条距离为定值的平行线上转化为基本问题;例4则是通过翻折变换和作垂线段，将折线段和的问题转化为基本问题.因此，转化思想在解决这类问题中显得尤为突出.几何中的最值问题形式多样，本文将此问题提炼出来，希望对读者有所启发.