利用一次函数解决相遇与追及问题

初二上学期最后一章是一次函数.这一章是学生在学习了位置与坐标后，进一步利用坐标系和一次函数的图像来解决实际生活中的一些问题.但是在教学中发现，很多学生只是简单的模仿，今天做类似的问题能够做对，明天将问题稍作改变，就会丈二和尚摸不到头脑了，特别是路程问题中的相遇和追及问题，学生学起来尤为困难.因此，本文选取了几个典型问题进行剖析，以便让学生更好的理解.

一、相遇问题

例1 一列快车从甲地开往乙地，一列慢车从乙地开往甲地，两车同时出发.设慢车的行驶时间x(h)，两车之间的距离为y(km)，图中的折线表示y与x之间的函数关系.根据图像(图1)进行以下探究：

(1)甲乙两地之间的距离为 ;

(2)请解释图中点B的实际意义；

(3)求慢车和快车的速度；

(4)求线段BC所表示的y与x之间的函数关系，并写出自变量x的取值范围.

例2 一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为y₁(km)，出租车离甲地的距离y₂(km)，客车行驶时间为x(h)，y₁，y₂与的函数关系图像如图2所示.

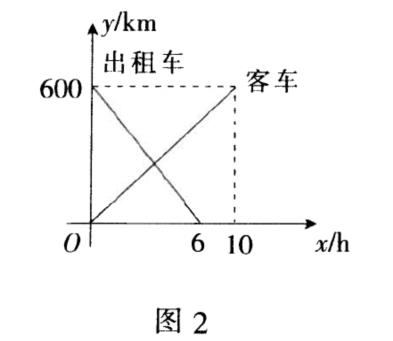
(1)根据图像，写出y₁与y₂与x的函数关系表达式；

(2)分别求出当x=3，x=5，x=8时，两车之间的距离；

(3)若设两车间的距离为s(km)请写出s关于x的函数关系式.

分析与解答

二、追及问题

例3 小明和小亮进行百米比赛，小明比小亮跑得快.如果两人同时起跑，小明肯定赢.现在小明让小亮先跑若干米.图6中l₁，l₂分别表示两人的路程与小明追赶的时间的关系.

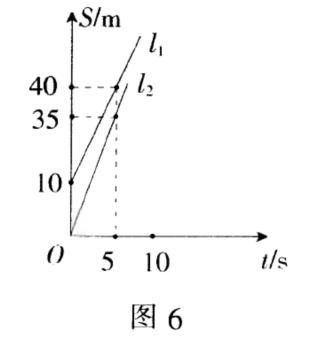
(1)哪条线表示小明的路程与时间的关系？

(2)小明让小亮先跑了多少米？

(3)谁将赢得这场比赛？

(4)对应的一次函数表达式中，一次函数的系数是多少？它的实际意义是什么？

三、总结

无论是相遇问题还是追及问题，只要认真审好题目，将题目中的问题和条件吃透，再分析图像的特征和数量关系，问题便会迎刃而解了甲切记，图像中的交点或拐点往往是问题解决的关键.