巧设未知数妙解三角形

三角形是平面内最简单的直线型封闭图形，是进一步探究学习其他图形的基础，对三角形有关的求解是初中数学教学中的重要内容.对于比较复杂的图形结构，其包含内角和，外角，等腰，直角，全等，平行，旋转，对称等角与角之间的关系，如何找出已知条件和所求角之间的关系是解题的关键.如果能巧设未知数，将已知条件转化成未知数的代数形式，并在图中表示出来，再结合代数方程思想来解决问题，就能起到事半功倍的效果.本文举例说明，在求解三角形有关角的问题时，如何巧设未知数，建立等量关系，再列方程求解的思路和方法.

一、巧设一个未知数，化繁为简

当题目中给出的角之间的等量关系比较密切时，可设其中一个角为x，其它它角就可以用x

的倍数来表示，并在图中标出来，最后结合三角形性质和题中所给条件列一元一次方程求解.

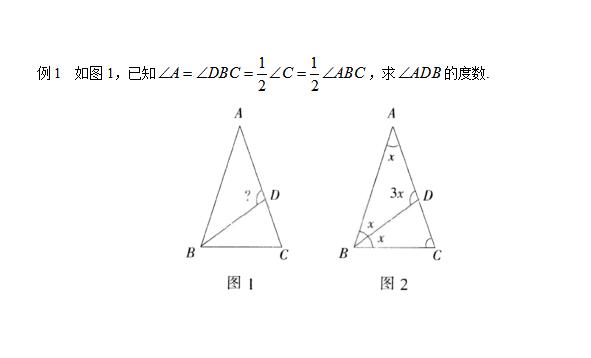
分析 题中给出了4个角的等量关系，因此，为便于计算，可设其中最小的角为x，则其他角都可以用x的倍数表示，如图2，最后以三角形内角和等于180º的性质为桥梁，建立等量关系，列出一元一次方程，求出x，从而求出∠ADB的度数.

二、巧设两个未知数，化隐为显

当题目所求的是两个角之间的等量关系，并非求某个角的具体度数时，可以设两个未知数，通过“设而不求”，以它们为中间变量，再根据三角形性质和已知条件，得出所求角之间的等量关系.

例2 如图5，BD、CD分别是三角形ABC的一个内角的角平分线和一个外角的角平分线，试探究∠A与∠B之间的等量关系.

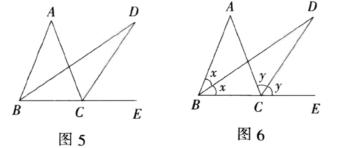
分析 由角平分线的知识，可知∠ABD=∠CBD，∠ACD=∠ECD，分别用未知数x、y

来表示，如图6.;再利用三角形一个外角等于与它不相邻两个内角之和的性质，构建∠A

和∠D之间的联系.

三、现学现用，化难为易

借助前面的介绍来解下面这道题.

例3 如图9，在三角形ABC中，AB=AC，AD=AE，∠BAE=60°，求∠EDC的度数.

分析1 题目中给出了两组边的等量关系，即给出了两组角的等量关系，可分别用x、y

来表示，如图10.通过三角形一个外角等于不相邻两个内角和的性质列出一元一次方程求解.

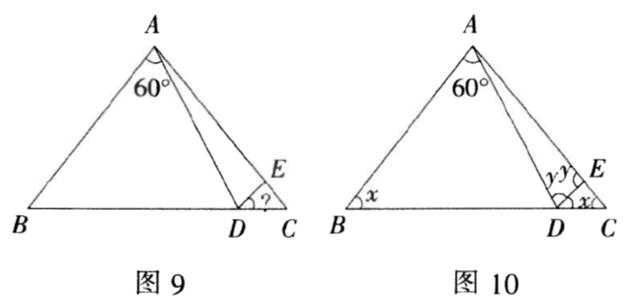
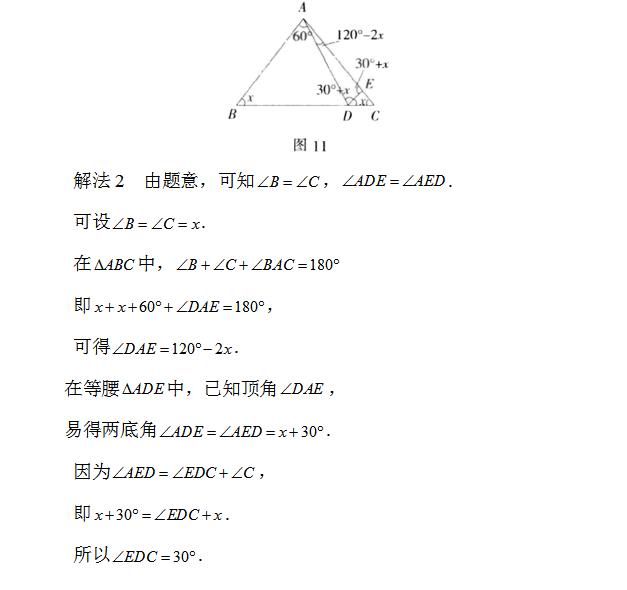
分析2 因为题中已知∠BAD=60°，也可以充分利用这一条件，只设一个未知数x

求解，如图11.

三角形中有关角的求解问题是初中平面几何中的重点，也是难点.笔者经过教学实践总结了一套比较实用的解题方法，即巧设未知数，运用代数方程思想将题中错综复杂的几何关系清晰的在图中标出来，从而找到解决问题的突破口，让学生在解题的过程中有一种“山重水复疑无路，柳暗花明又一村”的体验.