一次函数图像信息题

初中数学复习阶段中，学生对于图象信息题的解答正确率比较低.本文通过分析几个案例的特点，帮助大家探寻解决这些问题的关键.

一、拐点生图

案例1 (无锡市锡山区试题)一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地设先发车辆行驶的时间为xh，两车之间的距离为ykm当两车均到达各自终点时，运动停止.图1是

y与x之间函数关系的部分图象

(1)由图象知，慢车的速度为 km/h，快车的速度为 km/h;

(2)请在图中补全函数图象;

(3)求当x为多少时，两车之间的距离为300km.

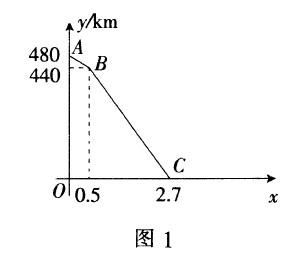
解析1 (1)这个试题从图象考虑拐点B，可以得到先开的车子0.5小时行驶了40km，得到速度为80km/h.考虑线段BC，我们可以看出从相距440km到相遇用了2. 2h，这时每小时缩短440 ÷2. 2=200km，得到另一车子速度为200－80=120km/h.这时得到慢车的速度为80km/h，快车的速度为120km/h.

(2)这里要探索出拐点，我们看一下车子达到目的地的时间:慢车为480 ÷ 80=6，快车为480÷120=4，快出晚开了0. 5小时，得到后面一个拐点的横坐标为4. 5，从2. 7－4. 5小时之间两辆车子相背而行，得到=200(X-2.7).当X=4.5时，有y=200×1.8=360,得到拐D(4.5,360).快车达到后，下一个终点为E(6,480)，画出图2.

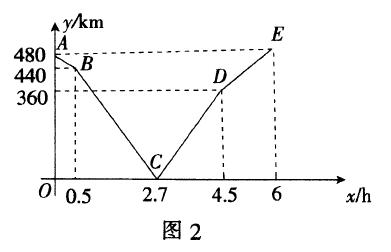
(3)由题意，可知两车行驶的过程中有2次两车之间的距离为300km.

设线段BC为y=kx+b.易得k=-200,b=540

于是，y=-200x+540.

当y=300时，得-200x+540=300，

∴x=1.2.

线段CD为y=200（x-2.7），

当y=300时，得200(x-2.7)=300，x=4.2.

故x=1.2h或4. 2 h，两车之间的距离为300km.

解析2 (2)我们知道图象中线段AB,BC从左到右边图象是下降的，也就是K<0.分别是－80、－200，相遇两车子距离逐步扩大，这时K>0.我们看一下车子达到目的地的时间:慢车为480÷ 80=6，快车为480÷120=4，快车晚开了0. 5小时，得到后面一个拐点的横坐标为4. 5，可以首先得到终点E(6,480).最后一段图象的函数表达式设为y=80x+b.将（6，4.8）代入，得到480=480+b，b=0，y=80x.当x=4.5，得到y=80×4.5=360，故D（4.5，360）.在图2中标出D,E，连结CD,DE，得到图2.

点评 这个题目中的(2)画出图象，关健是求出拐点的坐标.另一条隐藏的线索就是两车变化过程中有两段逐步缩小，两段逐步增加，这样可以为我们寻找拐点提供帮助.

二、一个有争议的解答

案例2 (无锡市八年级期末2016—2017年试题)已知甲、乙两地相距3200 m.小王、小李分别从甲、乙两地同时出发，相向而行，相遇后两人立即返回，回到各自出发地之后就停止行进.已知小李的速度始终是60m/min，在整个行进过程中，他们之间的距离y(m)与行进的时t(min )之间的函数关系如图中的折线段AB-BC-CD所示，请结合图象信息解答下列问题:

(1) a= , b= ;

(2)当t为何值时，小王、小李两人相距800 m?

解析 (1)这个问题中，AB代表同时出发，花20min相遇，相遇后两人立即返回，回到各自出发地之后就停止行进.这里小李速度没有变化，又是走原来的路，这说明他回到出发地相同，得到a-20=20,a=40;小王开始的速度为3200÷20－60=100m/min，后来速度为2800 ÷20－60=80，得到80(b-40)=3200-2800,b=45.

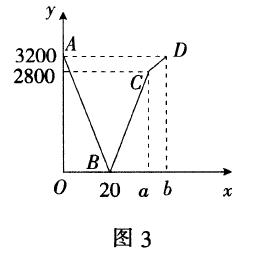
(2)设AB为y=kt+b.易得y=-160t+3200.

设BC为y=k₂t+b. 易得y=140t-2800.

当y=800时，

由-160t+3200=800，可得t=15；

由140t-2800=800，可得t=7/180.

综上，两人出发15min或7/180min时，相距800米.

另解:(1)有人认为小李晚到，b=40，这样可设CD为y=60t+b₁，以(40,3200)

代入，得3200=2400+b₁,b₁=800，故y=60t+800.当y=2800, 得60a=2000,a=33⅓.

(2)一个t仍然是15，设BC为y=k₂t+b₂.由B(20,0),C(3/100,2800),可求得y=210t-4200.

当y=800，得到t=500/21.

所以两人出发15 min或180/7 min时，相距800米.

点评 笔者认为原题中应该加“小王返回时速度减少”，这样才是原来提供的解析;如果加“小王返回速度增加”，那么是后面一种解答.否则结果应该是:

(1) a=40或33⅓，b=45或40;

(2) t=15，180/7或500/21，这样就不太合适了.