学完因式分解应具有四种意识及因式分解中的数学思想

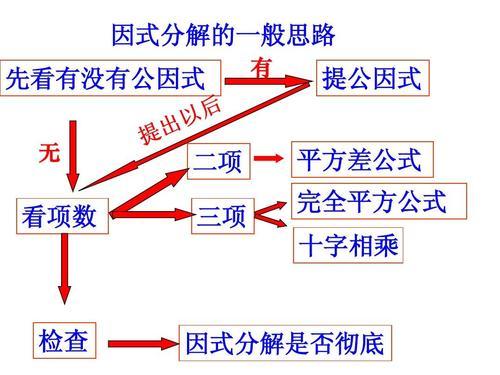
因式分解的顺序：①提公因式

②公式法（平方差公式，完全平方公式）

③十字相乘法（常用在二次三项式中不能完全平法的）

④分组分解法（常用在二次五项式中）

注：同学们在拿到一道因式分解的题目时要按照以上顺序思考，经过第一次分解以后仍要注意是否可以接着分解，例如（x+y）（x-y）可继续分解为（x+y）（x+y）（x-y）

学完因式分解应具有的四种意识

一、优先意识

按因式分解的一般步骤和思考程序，要树立优先提多项式公因式的意识

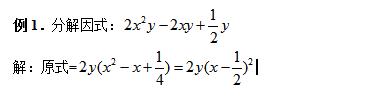
二、换元意识

通过换元，可以达到化繁为简、化难为易的目的

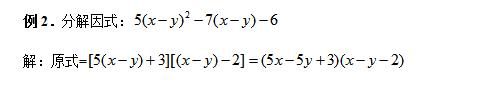
三、完整意识

依分解因式的步骤，因式分解必须分解到每个因式都不能再分解为止

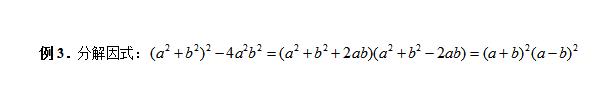
四、应用意识

因式分解中的数学思想

众所周知，数学思想是我们数学解题的灵魂，因式分解也不例外，在因式分解过程中也蕴含着许多的数学思想，如果能灵活的加以运用，往往能更好地解决因式分解问题，下面就因式分解中的常见的思想方法举例说明：

一、整体思想

所谓用整体思想来分解因式，就是将要分解的多项式中的某些项看成一个整体而加以分解.

二、类比思想

类比思想地因式分解中的运用很广泛，具体地表现在：一是因式分解与整式乘法的对比；二是因式分解与乘法的分配律的对比；三是因式分解与乘法公式的对比.

三、转化思想

转化思想就是对于某些多项式从表面是无法利用因式分解的一般步骤进行的，必须通过适当的转化，如经过添项、拆项等变形，才能利用因式分解的有关方法进行.

四、换元思想

所谓的换元就是将多项式的某些项用另一个新的字母去代换，通过换元可以将复杂的多项式转变成简单的，将陌生的转换成熟悉的，使之得以顺利地分解因式.