【专题点拨】
动态型问题一般是指以几何知识和图形为背景,渗透运动变化观点的一类试题,常见的运动对象有点动、线动和面动;其运动形式而言就是平移、旋转、翻折和滚动等。
动态型试题其特点是集几何、代数知识于一体,数形结合,有较强的综合性,题目灵活,多变,动中有静,动静结合,能够在运动变化中发展同学们的空间想象能力。
解答动态型试题的策略是:
(1)动中求静,即在运动变化中探索问题中的不变性;
(2)动静互化,抓住静的瞬间。找到导致图形或者变化规律发生改变的特殊时刻,同时在运动变化的过程中寻找不变性及其变化规律。
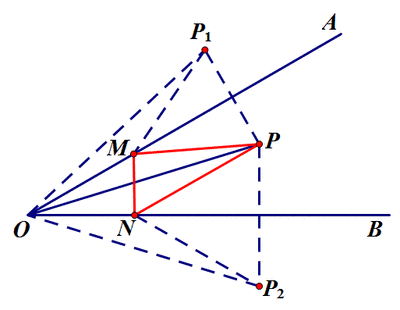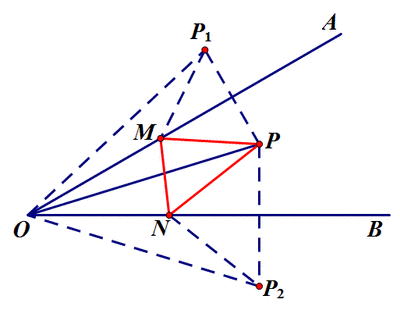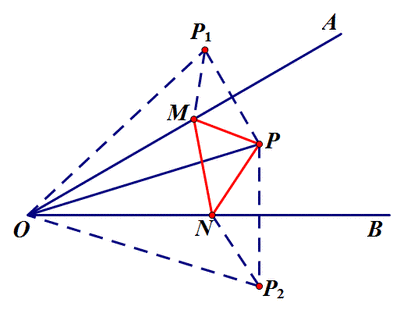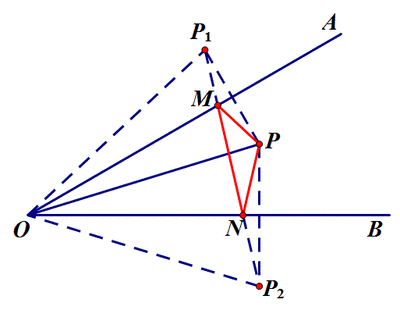
【典例赏析】

【解答】解:∵四边形ABCD是正方形,
∴AB=CD,∠BAD=∠ADC=90°,∠ADB=∠CDB=45°,
在△ABE和△DCF中,
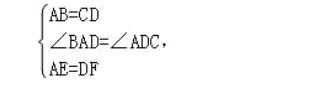
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
在△ADG和△CDG中,
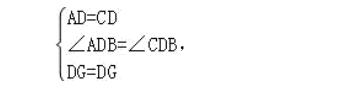
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCF,
∴∠ABE=∠DAG,
∵∠DAG+∠BAH=90°,
∴∠BAE+∠BAH=90°,
∴∠AHB=90°,
∴AG⊥BE,故③正确,
同法可证:△AGB≌△CGB,
∵DF∥CB,
∴△CBG∽△FDG,
∴△ABG∽△FDG,故①正确,
∵S△HDG:S△HBG=DG:BG=DF:BC=DF:CD=tan∠FCD,
又∵∠DAG=∠FCD,
∴S△HDG:S△HBG=tan∠FCD,tan∠DAG,故④正确
取AB的中点O,连接OD、OH,
∵正方形的边长为4,
∴AO=OH=1/2×4=2,
由勾股定理得,OD=2·根号5,
由三角形的三边关系得,O、D、H三点共线时,DH最小,
DH最小=2·根号5﹣2.
无法证明DH平分∠EHG,故②错误,
故①③④⑤正确,
故选C.
【考点解析】
考点一:相似三角形的判定与性质;
考点二:全等三角形的判定与性质;
考点三:正方形的性质;
考点四:解直角三角形.
【解题思路】
首先证明△ABE≌△DCF,△ADG≌△CDG(SAS),△AGB≌△CGB,利用全等三角形的性质,等高模型、三边关系一一判断即可.
【考点点评】
此题考察的是点动引起的线动问题,考察的并不难,主要抓住运动中的不动,即无论E、F怎么动,△ABE和△DCF,△AGB和△CGB,△ADG和△CDG永远是全等的,在利用全等性质结论显而易见。
同学们做出来了吗?大家可以尝试做一做下面这道题。
【课后习题】
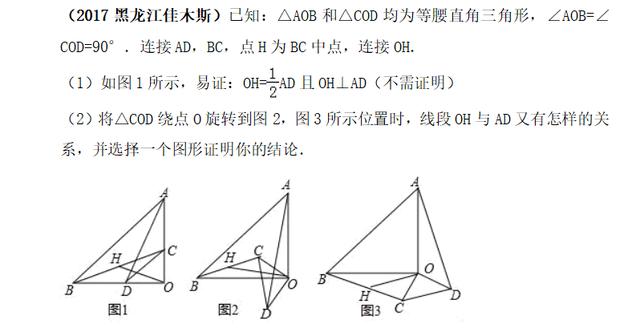

 加载中,请稍侯......
加载中,请稍侯......
精彩评论