高考数学精讲知识点（2）：四种命题、充要条件

【考点梳理】

一、命题：可以判断真假的语句。

二、四种命题

三、四种命题的相互关系及其等价性

1、四种命题的相互关系

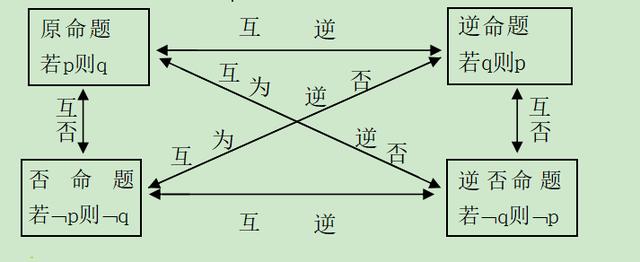
2、互为逆否关系的命题同真同假，即原命题与逆否命题的真假性相同，原命题的逆命题和否命题的真假性相同。所以，如果某些命题（特别是含有否定概念的命题）的真假性难以判断，一般可以判断它的逆否命题的真假性。

四、充分条件、必要条件和充要条件

【典型例题】

类型一：四种命题及其关系

例1. 写出命题“已知是实数，若ab=0，则a=0或b=0”的逆命题，否命题，逆否命题，并判断其真假。

解析：逆命题：已知是实数，若a=0或b=0, 则ab=0, 真命题；

否命题：已知是实数，若ab≠0，则a≠0且b≠0，真命题；

逆否命题：已知是实数，若a≠0且b≠0，则ab≠0，真命题。

点评：

1.“已知是实数”为命题的大前提，写命题时不应该忽略；

2. 互为逆否命题的两个命题同真假；

3. 注意区分命题的否定和否命题.

举一反三：

理数

”.假命题.

(3)的否定是“∀α，β∈R，使sin(α＋β)≠sinα＋sinβ”.假命题.

(4)的否定是“∀x，y∈Z，使3x－2y＝10”.假命题.

类型二：充要条件的判断

例2.设有两个命题：p：x2－2x＋2≥m的解集为R；q：函数f(x)＝－(7－3m)x是减函数，若这两个命题中有且只有一个是真命题，求实数m的取值范围．

解析：若命题p为真命题，可知m≤1；

若命题q为真命题，则7－3m>1，即m<2.

所

以命题p和q中有且只有一个是真命题时，有p真q假或p

假q真，即

点评：

1. 处理充分、必要条件问题时，首先要分清条件与结论；

2. 正确使用判定充要条件的三种方法，要重视等价关系转换.

举一反三：

.

举一反三：

点评：从认知已知条件切入，将四种命题或充要条件问题向集合问题转化，是解决这类问题的基本策略。