高考数学精讲知识点（6）：二次函数与幂函数

【知识网络】

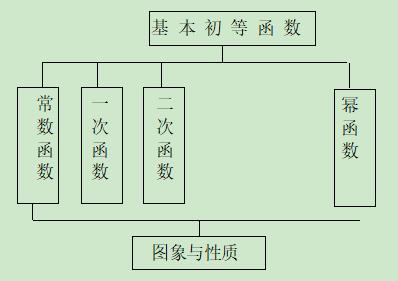
【考点梳理】

考点一、初中学过的函数

（一）函数的图象与性质

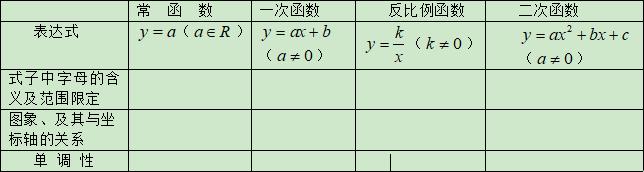
要点诠释：

1.过原点的直线的方程,图象,性质；

2.函数的最高次项的系数能否为零。

（二）二次函数的最值

1.二次函数有以下三种解析式：

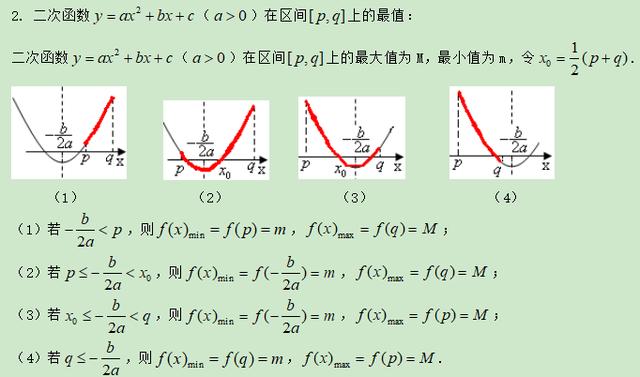
要点诠释：

1．二次函数的最值只可能在三处取得：两个区间端点以及顶点的函数值；

2. 求二次函数的最值一般要数形结合。

考点二、幂的运算

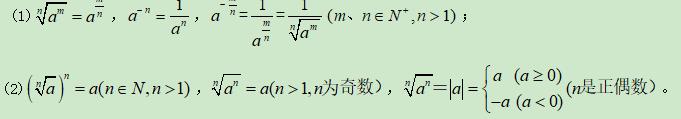
考点三、幂函数的图象与性质

要点诠释：幂函数在第四象限没有图象，其它象限的图象可以由奇偶性确定。

【典型例题】

类型一：基本函数的解析式

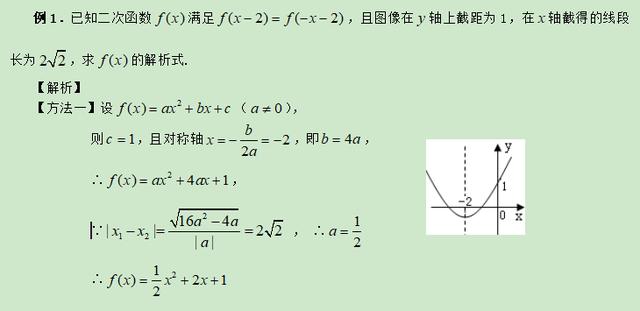
【总结升华】二次函数的形式有以下三种：

举一反三：

类型二：函数的图象和性质

举一反三：

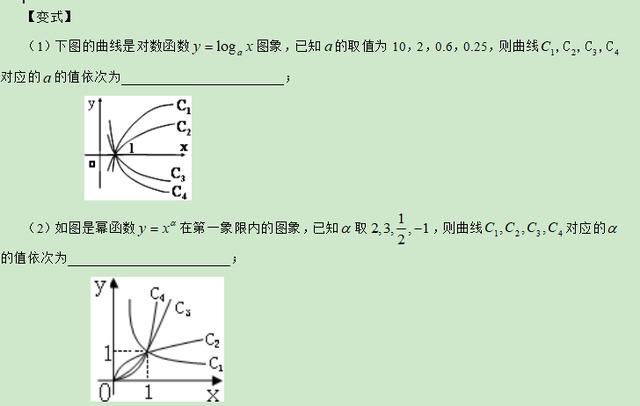
类型三：比较大小

【总结升华】大小比较是此处常见的一类考题。通常都是构想函数运用函数性质来解决，通常两个同指的幂式比较就构想幂函数，同底的就构想指数函数，若混合比较即插入对数式或底指皆不同的幂式就用搭桥的办法，常用搭桥的思路有选0或选1或根据具体情况构作。

举一反三：

类型四：最值问题

举一反三：