高考精讲知识点（13）：定积分和微积分基本定理

【知识网络】

【考点梳理】

要点一、定积分的概念

要点诠释：

（1）定积分的值是一个常数，可正、可负、可为零；

（2）用定义求定积分的四个基本步骤：①分割；②近似代替；③求和；④取极限.

要点二、定积分的性质

要点三、微积分基本定理

要点诠释：

求定积分主要是要找到被积函数的原函数，也就是说，要找到一个函数，它的导函数等于被积函数.由此，求导运算与求原函数运算互为逆运算.

要点四、定积分的几何意义

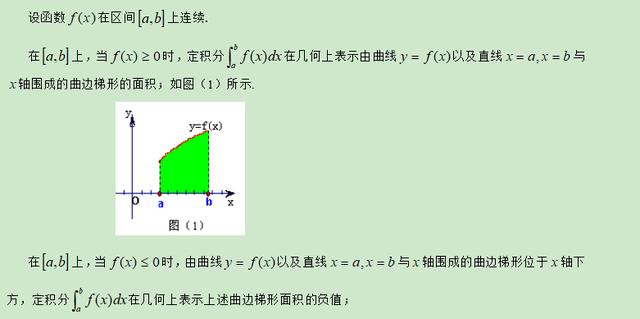
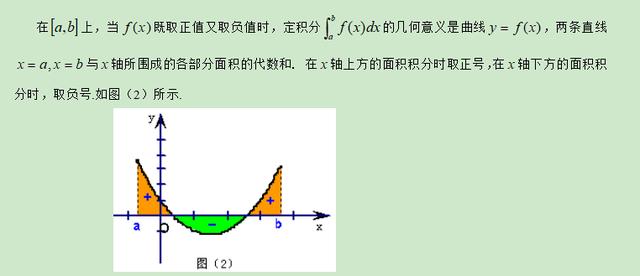
要点五、应用

（一）应用定积分求曲边梯形的面积

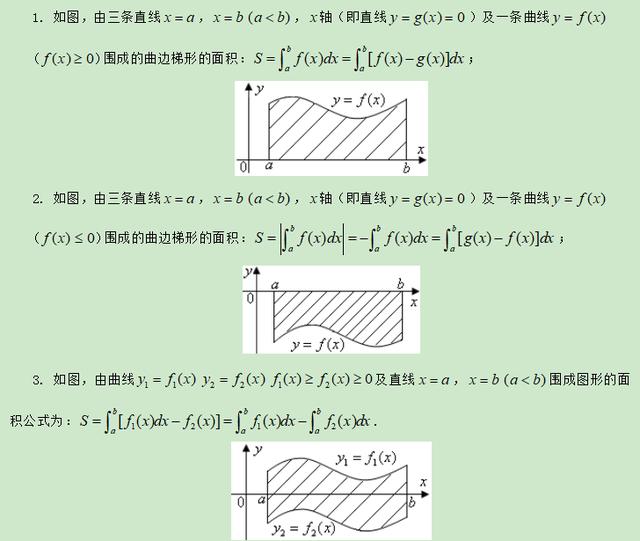
4.利用定积分求平面图形面积的步骤：

（1）画出草图，在直角坐标系中画出曲线或直线的大致图像；

（2）借助图形确定出被积函数，求出交点坐标，确定积分的上、下限；

（3）写出定积分表达式；

（4）求出平面图形的面积.

（二）利用定积分解决物理问题

【典型例题】

类型一：运用微积分定理求定积分

举一反三：

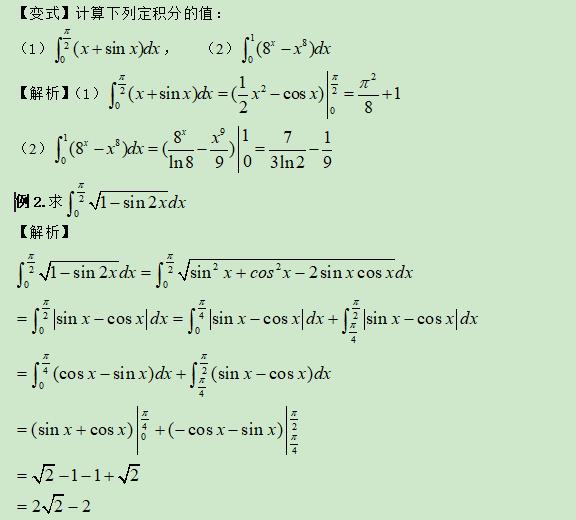
【总结升华】化简被积函数是积分的前提，直到最简为止.

举一反三：

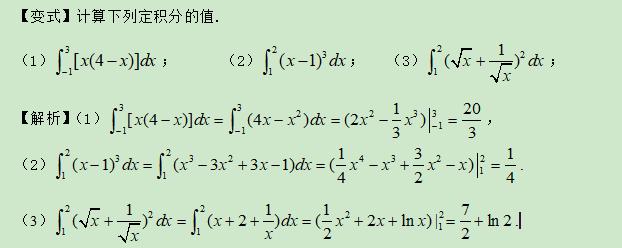
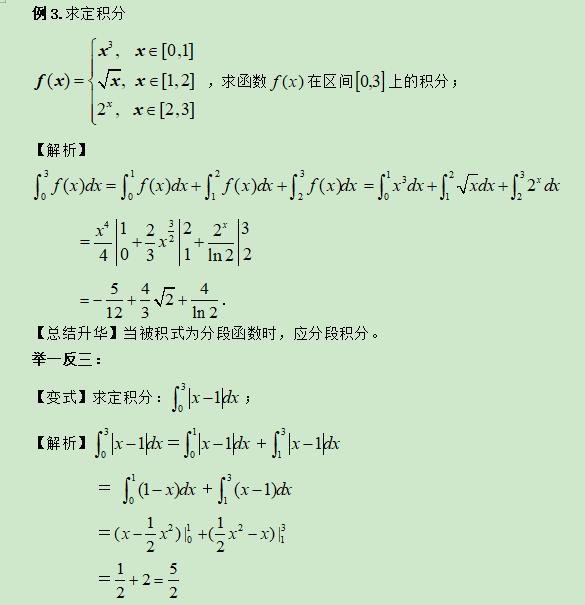
类型二：利用定积分的几何定义

类型三：利用定积分求平面图形面积

举一反三：

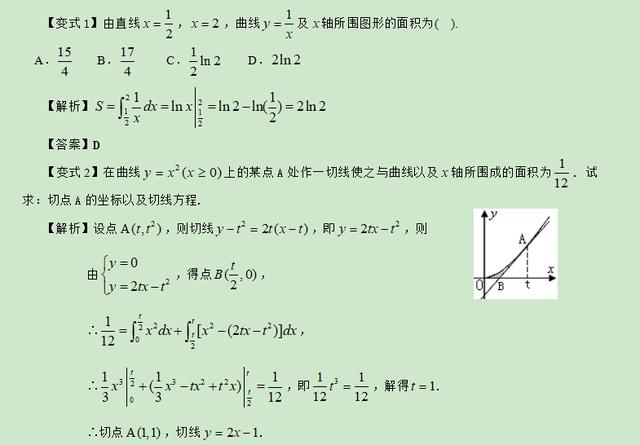
类型四：利用定积分解决物力问题