高考知识点精讲（19:）：三角函数的最值与综合应用

【知识网络】

【考点梳理】

考点一、三角函数的最值

求三角函数的值域，除了判别式、重要不等式、单调性等方法之外，结合三角函数的特点，还有如下常用方法：

要点诠释：

三角函数的最值问题，其本质是对含有三角函数的符合函数求最值，因此求函数最值的方法都能使用．当然也要掌握上述的特殊的方法.

要点诠释：

求三角函数的单调区间、周期，及判断函数的奇偶性，要注意化归思想的运用，通过恒等变换转化为基本三角函数类型，注意变形前后的等价性.

考点三、用三角函数解决一些简单的实际问题

三角函数的知识产生于测量、航海和天文学，还在机械制造、电工学、物理学等学科中有着广泛的应用.对于测量中的问题，要理解有关仰角、俯角、方位角、方向角的概念；对几何问题，特别是立体几何中的问题，要依据题意，画出示意图或立体直观图，将问题归结到三角形中去处理.一般情况下，只要构成三角形就可直接应用三角函数的概念和解三角形的知识解决问题，对于一些较为复杂的应用题则需综合应用代数、立体几何或解析几何知识来解.此外，有些应用题在解答过程中使用三角代换可以简化解题过程，使对数值的处理更为方便.

【典型例题】

类型一：三角函数的最值

举一反三：

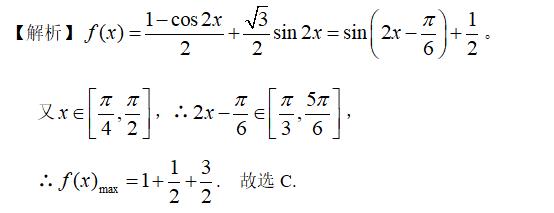
举一反三：

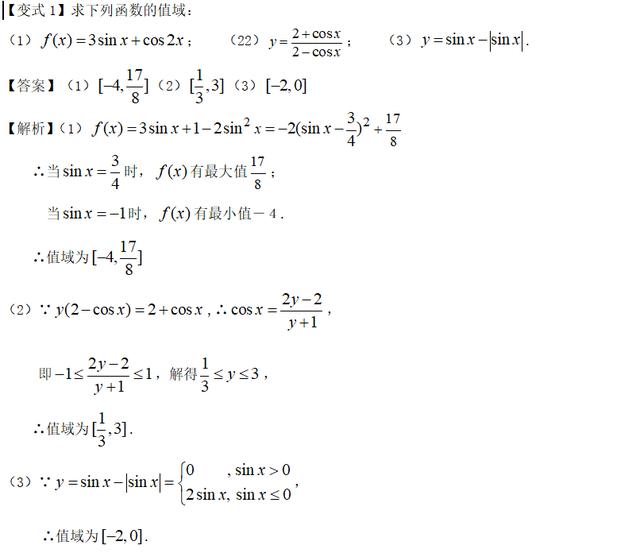
举一反三：

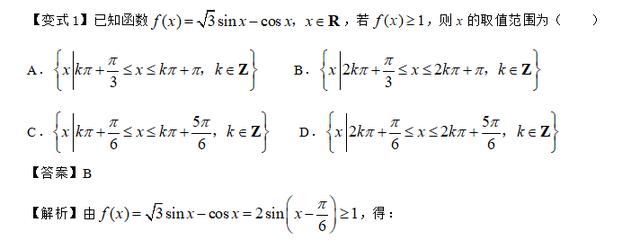
举一反三：

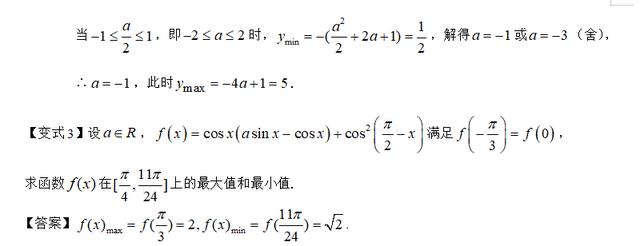
类型三：三角函数在实际生活中的应用

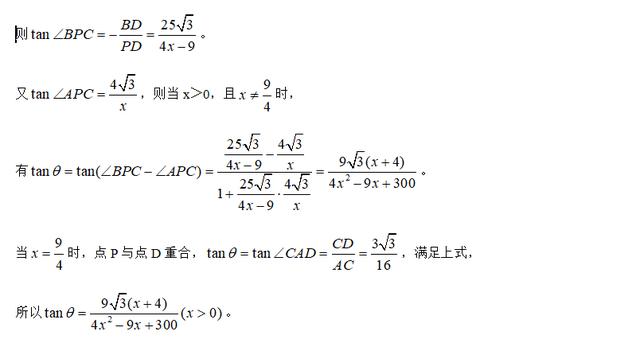
举一反三：