高考知识点精讲（21）平面向量的概念、线性运算及坐标运算

【知识网络】

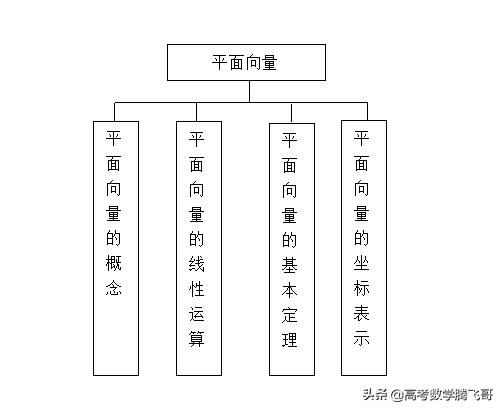
【考点梳理】

考点一、向量的概念

要点诠释：

考点二、向量的加法、减法

1．向量加法的平行四边形法则

2．向量加法的三角形法则

3. 向量的减法

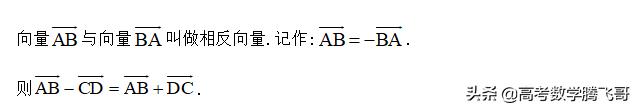
要点诠释：

①关于两个向量的和应注意：两个向量的和仍是一个向量；使用三角形法则时要注意“首尾相连”；当两个向量共线时，三角形法则适用，而平行四边形法则不适用.

②向量减法运算应注意：向量的减法实质是加法的逆运算，差仍为一个向量；用三角形法则作向量减法时，记住“连结两个向量的终点，箭头指向被减向量”.

要点三、实数与向量的积

要点诠释：

考点四、平面向量的坐标运算

要点诠释：

【典型例题】

类型一、平面向量的相关概念

【总结升华】

从向量的定义可以看出，向量既有代数特征又有几何特征，因此借助于向量可将代数问题与几何问题相互转化。零向量是一特殊向量，它似乎很不起眼，但又处处存在。因此，正确理解和处理零向量与非零向量之间的关系值得我们重视。对于平行向量或共线向量，它们可以在同一直线上，也可以所在直线互相平行，方向可以相同也可以相反；相等向量则必须大小相等、方向相同。

举一反三：

类型二、平面向量的加减及其线性运算

举一反三：

【总结升华】

①证明三点共线问题，可以用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得到三点共线.

②向量共线的充要条件中要注意当两向量共线时，通常只有非零向量才能表示与之共线的其他向量，要注意待定系数与方程思想的运用.

举一反三：

类型三、平面向量的基本定理、坐标表示及综合应用

举一反三：

【总结升华】关注三角形的“心”，包括三角形的重心、垂心、外心、内心和旁心.

举一反三：