高考知识点精讲（22）：平面向量的数量积及应用

【知识网络】

【考点梳理】

考点一、向量的数量积

1. 定义：

要点诠释：

2. 平面向量的数量积的几何意义

要点诠释：

3. 性质：

4. 运算律

要点诠释：

5. 向量的数量积的坐标运算

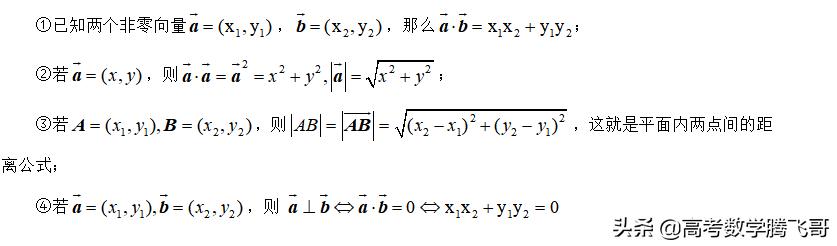
6. 重要不等式

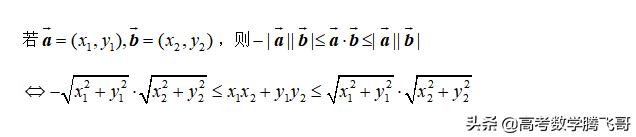
考点一、向量的应用

【典型例题】

类型一、数量积的概念

举一反三：

【总结升华】考查平面向量数量的角度问题，注意运用数量积的运算性质及夹角的范围，公式合理的选用有助于分析解决问题.

举一反三：

【总结升华】考查平面向量数量积和模的问题，考查我们运用知识分析解决问题的能力. 注意本题是转换为代数运算求最值问题.

举一反三：

类型二、数量积的综合应用

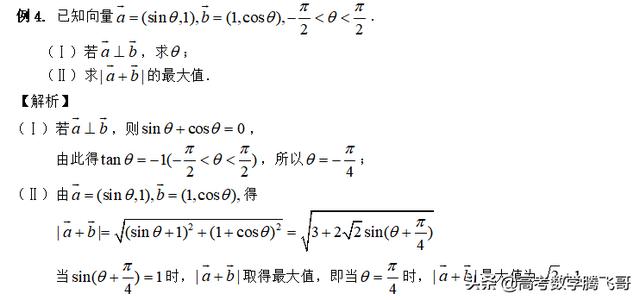
【总结升华】平面向量有几何和代数两种形式，并通过平面直角坐标系将它们联系起来，所以可以说，向量实际上是解析几何的内容，它把数形很好地结合在一起，这正是数学学习中的一个重要思想方法，因此在解决数学问题时被广泛应用.高考中，除了对平面向量本身的概念、运算加以考察外，更重要的是他与其他知识的联系，即用向量来解决代数、几何等综合问题，从而考察学生综合解决问题的能力.

举一反三：