高考知识点精讲（24）数列的概念

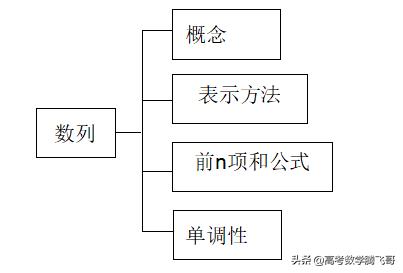
【知识网络】

【考点梳理】

考点一：数列的概念

按照一定顺序排列着的一列数称为数列.

数列中的每一个数叫做这个数列的项.各项依次叫做这个数列的第1项，第2项，…；排在第

位的数称为这个数列的第

项.其中数列的第1项也叫作首项。

要点诠释：

⑴数列的数是按一定次序排列的，因此，如果组成两个数列的数相同而排列次序不同，那么它们就是不同的数列；

⑵定义中并没有规定数列中的数必须不同，因此，同一个数在数列中可以重复出现.

考点二：数列的表示

(1)列举法：如-2，-5，-8，…

(2)图象法：由点

组成的图象；是离散的点集。

(3)解析式法：类似于函数的解析法，数列的解析法就是给出了数列的通项公式an=f(n)，n∈N*。

(4)递推：利用数列的第n项与它前面若干项的关系及初始值确定。如an=an-1+an-2(n≥3)，且a1=1，a2=1.

要点诠释：

①并不是每个数列都能写出它的数列通项公式；数列的通项如果存在，也不一定唯一。

②数列的列举法与集合的列举法不一样，主要就是有序与无序的差别。

③利用递推关系表示数列时，需要有相应个数的初始值。

考点三：数列的分类

（1）按项数：有限数列和无限数列

（2）按单调性：常数列、摆动数列、单调数列(递增数列、递减数列)

考点四：数列的通项公式与前你n项和公式

【典型例题】

类型一：依据数列的前几项的值，写出数列的一个通项公式

举一反三：

类型二：数列的递推关系式

【总结升华】求数列通项公式，特别是由递推公式给出数列时，除迭加、迭代、迭乘外还应注意变形式是否是等差（等比）数列.对于数列递推公式不要升温，只要能根据递推公式写出数列的前几项，由此来猜测归纳其构成规律.

举一反三：

举一反三：

类型四：数列的单调性

举一反三：