高考数学：函数与导数压轴题高频考点与破解妙招

1以导数面目包装的函数性质的综合应用

有关函数与导数的小题压轴题是新课标全国卷的高频考题，高频题型：①以导数面目包装的函数性质题(单调性、奇偶性、最值等)；②用导数法判断函数f(x)的图象或已知函数图象求参数的取值范围；③函数与集合、不等式、数列、平面向量、新定义等知识相交汇．

【命题意图】本题主要考查函数与导数、函数的单调性、函数的最值、函数的零点等知识，意在考查考生的化归与转化能力、数形结合能力和运算求解能力．

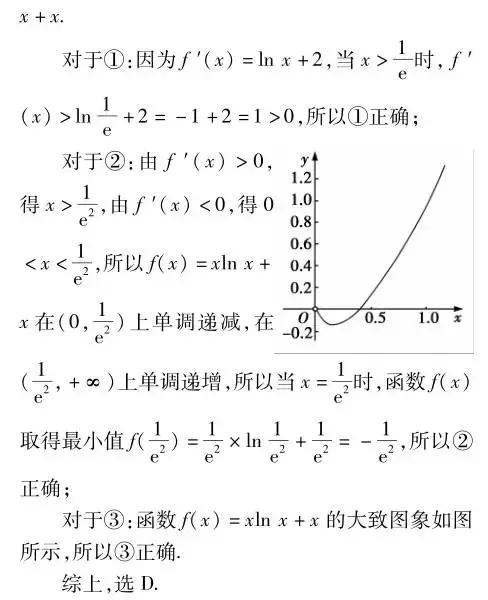
【攻略秘籍】　破解以导数面目包装的函数性质综合题需过双关：第一关是“还原关”，即先还原出函数的解析式；第二关是“数形关”，即不等式恒成立问题与有解问题多需要数形结合，即可轻松解决．

2利用导数研究函数的单调性、极值与最值

利用导数研究函数的单调性、极值与最值是高考的一棵“常青树”， 高频题型：①判断函数f(x)的单调性或求函数f(x)的单调区间；②求函数f(x)的最值或极值；③由函数的单调区间、最值或极值求参数的值．

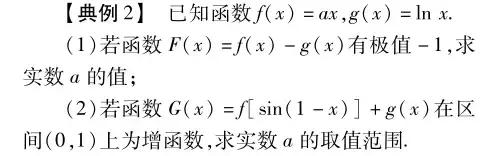
【命题意图】本题主要考查函数的极值、利用函数的单调性求参数的取值范围，意在考查分类讨论思想和方程思想，考查考生的化归与转化能力、运算求解能力．

【攻略秘籍】破解此类题的关键：一是方程思想，即对于含有参数的可导函数有极值的关键是对参数进行分类讨论，并寻找其导数为零的根，以及在根的左、右两侧导数的符号；二是转化思想，即可导函数f(x)在某个区间D内单调递增(或递减)，则有f ′(x)≥0(或f ′(x)≤0)在区间D内恒成立，从而把已知函数的单调性问题转化为恒成立问题来解决，这里需注意“＝”的情形．

3函数、导数与零点相交汇

如稍加留神，便可以发现，函数、导数与函数的零点(方程的根)相交汇的考题在近年的高考中扮演着重要的角色，高频题型：①判断函数的零点(方程的根)的个数问题；②已知函数在给定区间的零点(方程在给定区间的解)的情况，求参数的取值范围或证明不等式成立．

【命题意图】本题主要考查函数的零点、函数的最值、导数及其应用、基本不等式等知识，考查推理论证能力、运算求解能力、创新意识．

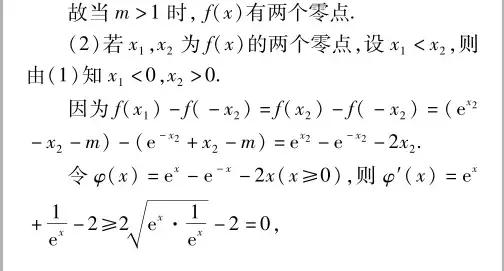
【攻略秘籍】　破解此类难题要过好三关：第一关，应用关，即利用导数法求函数的单调区间与最值，一般是求导数，在定义域范围内，令导函数大于(小于)零，得其单调递增(减)区间，从而求出函数的单调区间，再由函数的单调性，可求其最值；第二关，转化关，即把判断函数的零点个数问题转化为判断函数最值的符号问题；第三关，构造函数关，即通过构造函数，把比较大小问题转化为判断函数的单调性问题．

4函数、导数与不等式相交汇

函数、导数与不等式相交汇的试题是2015年高考题中比较“抢眼”的一种题型．对于只含有一个变量的不等式问题，常通过构造函数，利用函数的单调性和极值来证明，高频题型：①用导数法解决含参不等式恒成立问题；②用导数法解决含参不等式有解问题；③证明不等式．

【命题意图】　本题主要考查函数的单调性与极值点、不等式恒成立问题、证明不等式等知识，考查推理论证能力、运算求解能力，考查函数与方程思想、化归与转化思想、分类与整合思想．

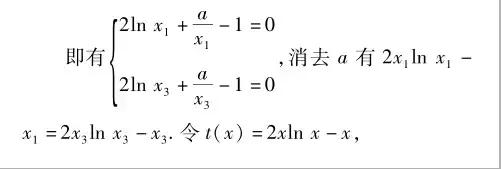
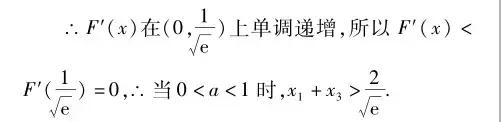
【攻略秘籍】　破解此类不等式证明的关键是通过构造函数、利用导数法判断函数的单调性来证明不等式．根据题设条件的结构特征构造一个函数，一是需要预设与所证不等式有相同的结构；二是需要熟练掌握简单复合函数的求导变换．不等式恒成立求参数的取值范围常利用“分离参数法”，也可以单刀直入地利用导数法，通过分类讨论使问题获解．注意恒成立问题与能成立问题的区别．

从以上四例可以看出，只要我们对“函数与导数类”压轴题常见类型心中有数，把握其实质，掌握其规律，规范其步骤，做到“胸中有法”，那么不论高考“函数与导数类”压轴题的构思多么新颖，我们都能做到以不变应万变，此类压轴题就能迎刃而解．