初中数学-必考类型-将军饮马

在初中数学中，经常会考到求线段最值、求路线最值、周长最值的问题。这种题型近几年来更是中考的热门考题。

这种问题涉及到的一个重要几何模型就是将军饮马模型。

将军饮马指的是：一位将军从营地A出发，外出去B地巡视边防。在B地巡视完边防后，要在天黑之前赶回营地A处。但是由于战马长途奔袭，体力不及，所以将军要先带着战马去远处的一条小河喝水。然后才能继续返回营地A处。（A.B，小河三地不再同一个直线上），现在将军要选一条最近的路线，才能在天黑之前返回营地。所以将军要带着战马去河边的哪一个位置饮水，才能使所走的路线最短？

在数学中，我们也将细细的求线段最值、路线最值、周最值的题型称之为将军饮马题型。

下面是将军饮马题型的实题，通过实题我们来学习以下将军饮马题型的求法，和解题思路。

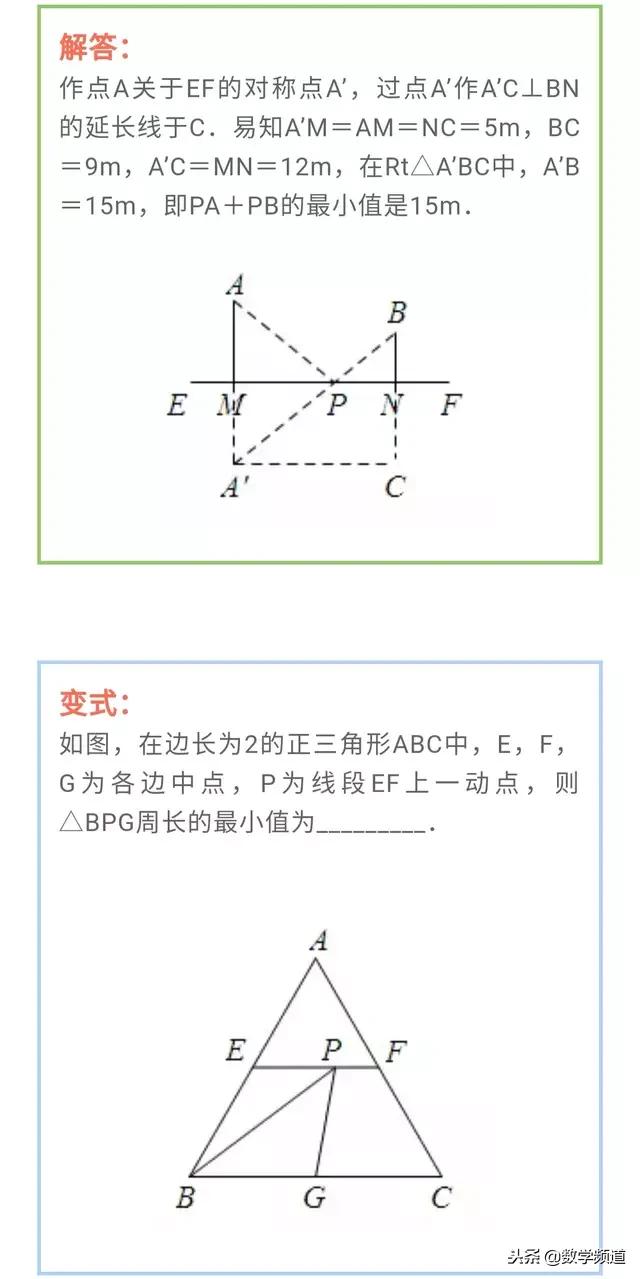
两定一动模型，是指有两个点是定点，不发生变动，而另外一个点是不确定点，有待我们确定的模型。这种模型是典型的将军饮马模型。这种题型相对来说比较简单，学生可以直观的找出答案。

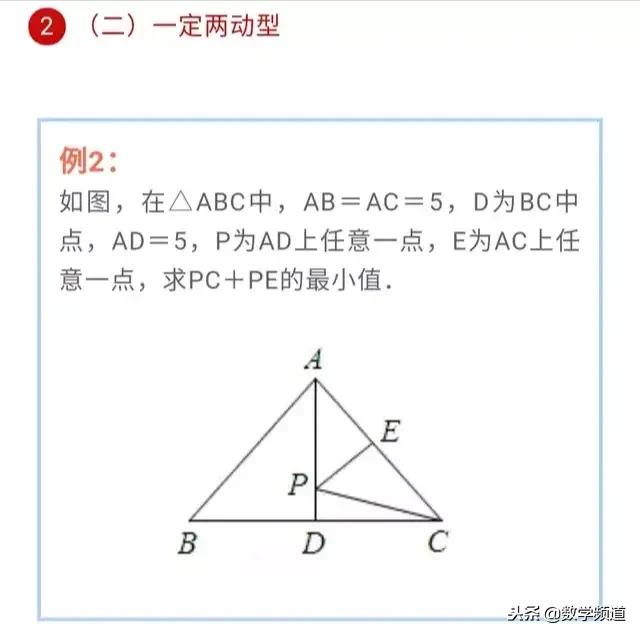
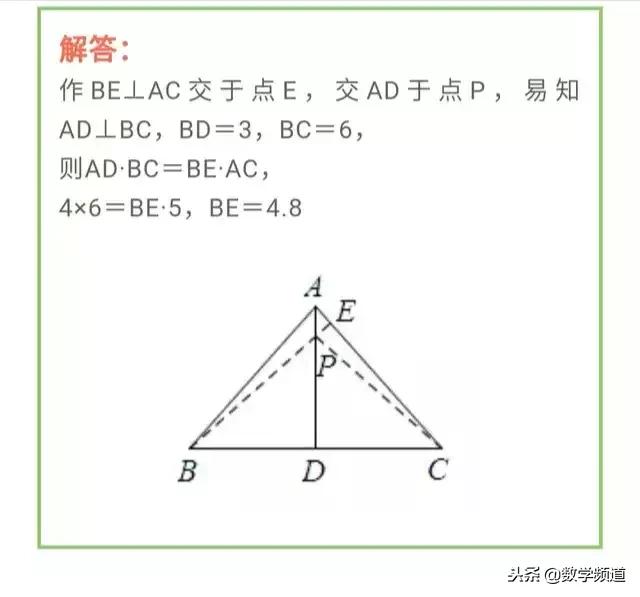
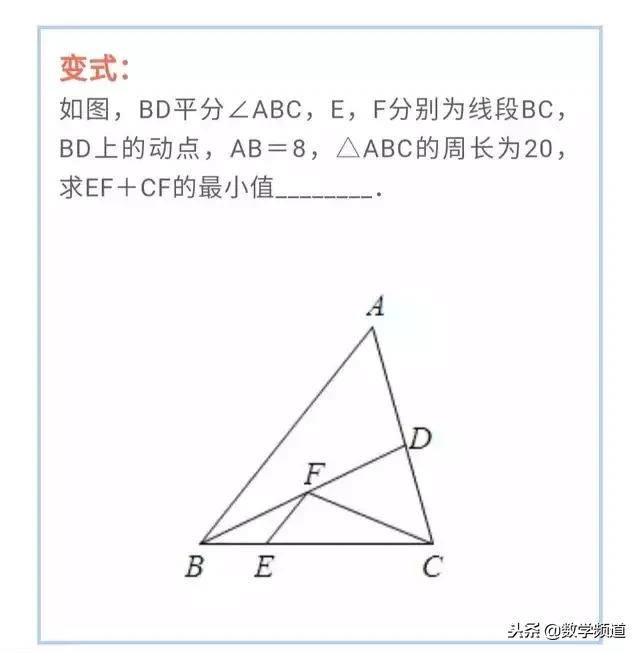
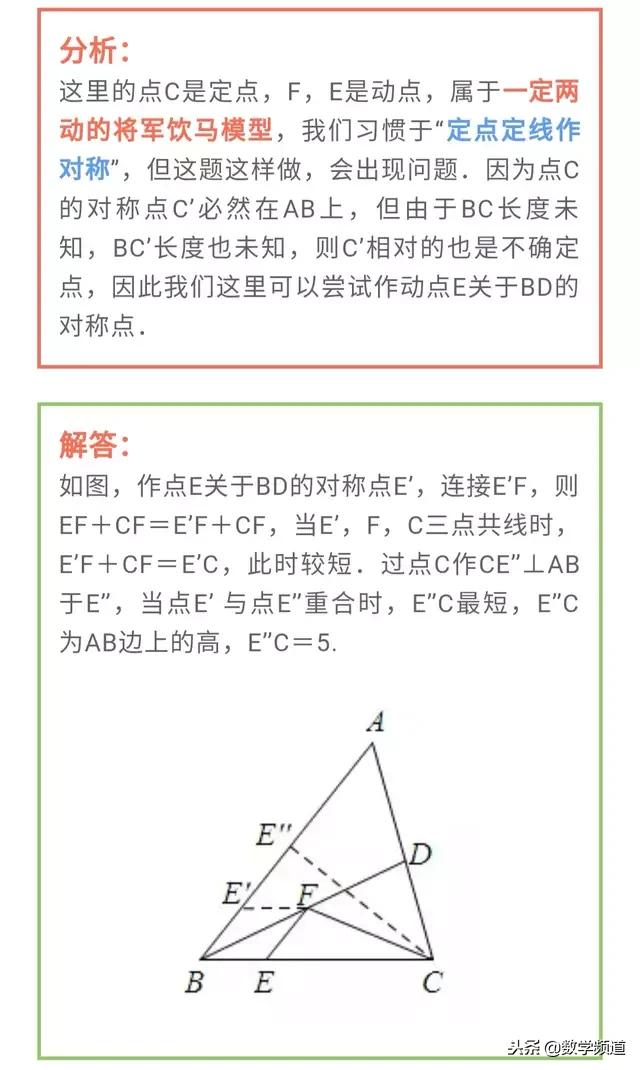
一定两动模型，是指三个点中，只有一个点是固定不变的，另外两个点是在运动的。由于另外两个点在变动，所以三点之间所成线段的长度和也是发生变化的。但是在运动过程中，一定会存在一个位置，使三点之间的长度和最短。而让我们求的就是这个最短值。折中题型是将军饮马模型的变形。相对来说有一定难度。

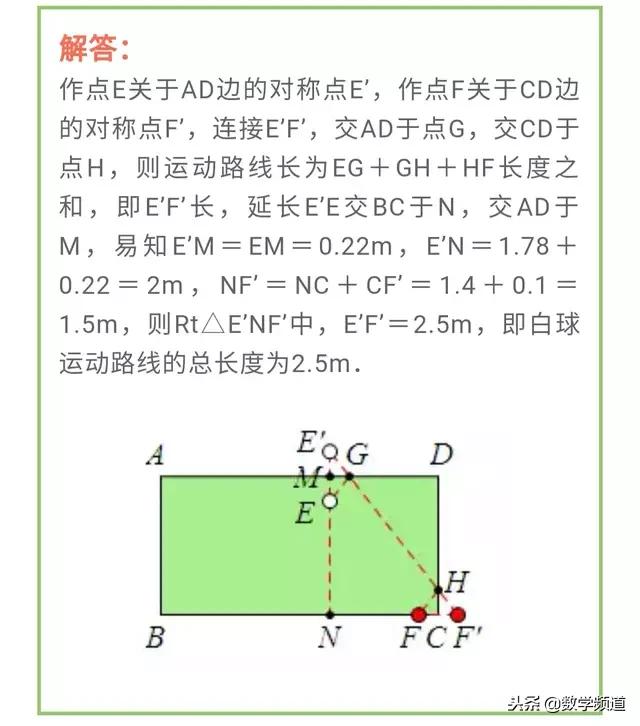
两静两动模型，是将军饮马模型的延伸。将原来的三个点之间的线段和问题，延伸成了四个点之间的线段求和。这种题型同样是找出定点的对称点，然后利用两点之间线段最短的理论去求解，找出最短距离。

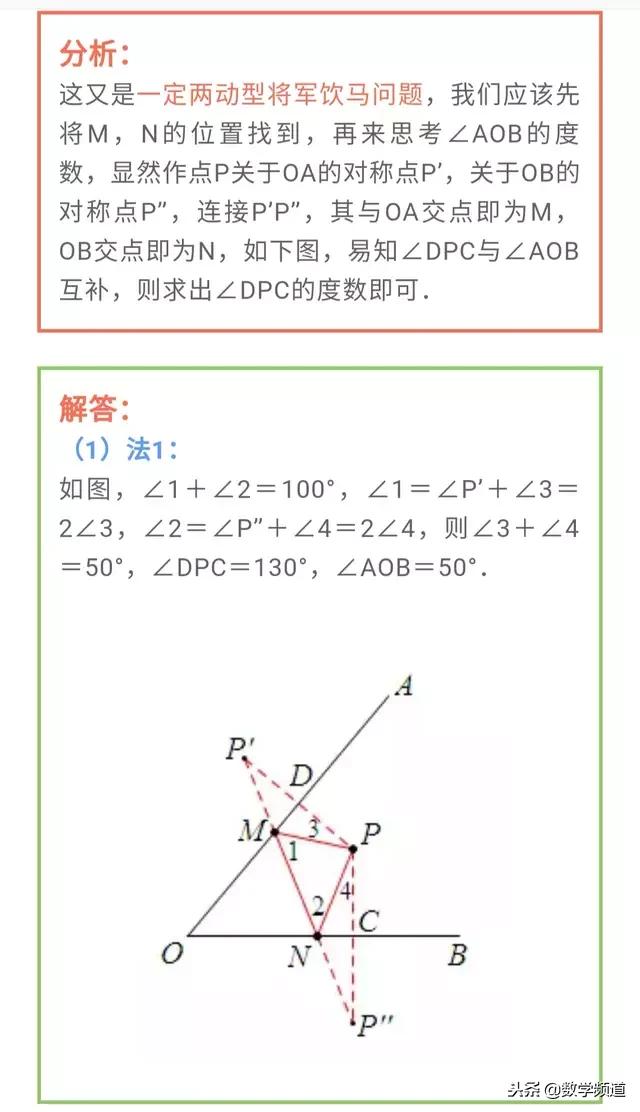
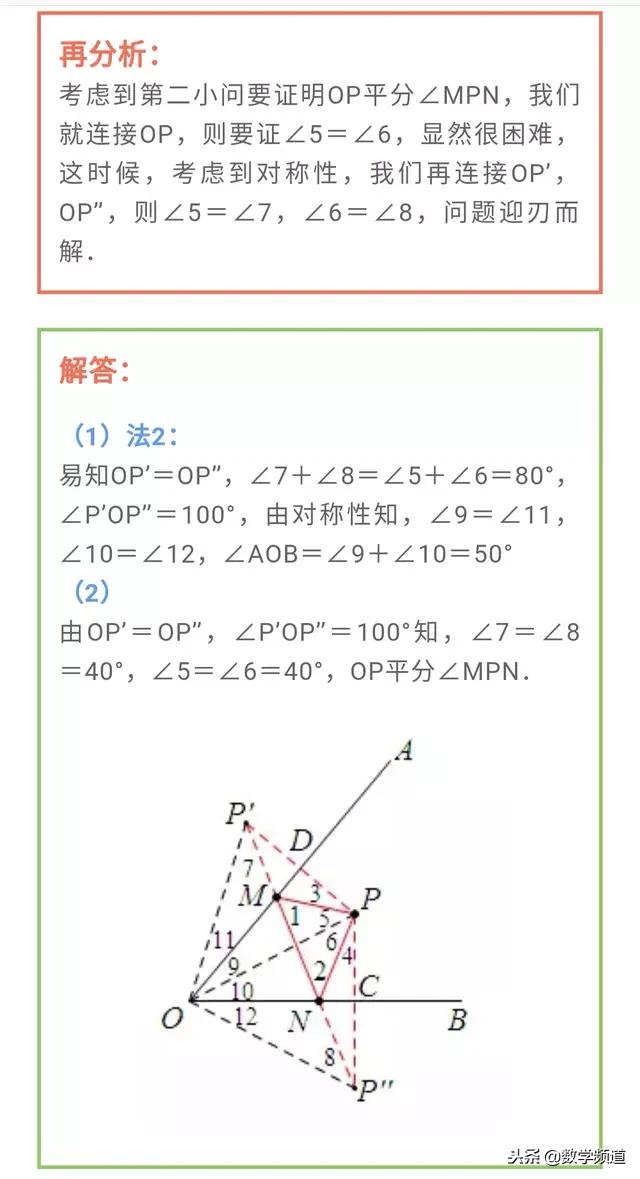
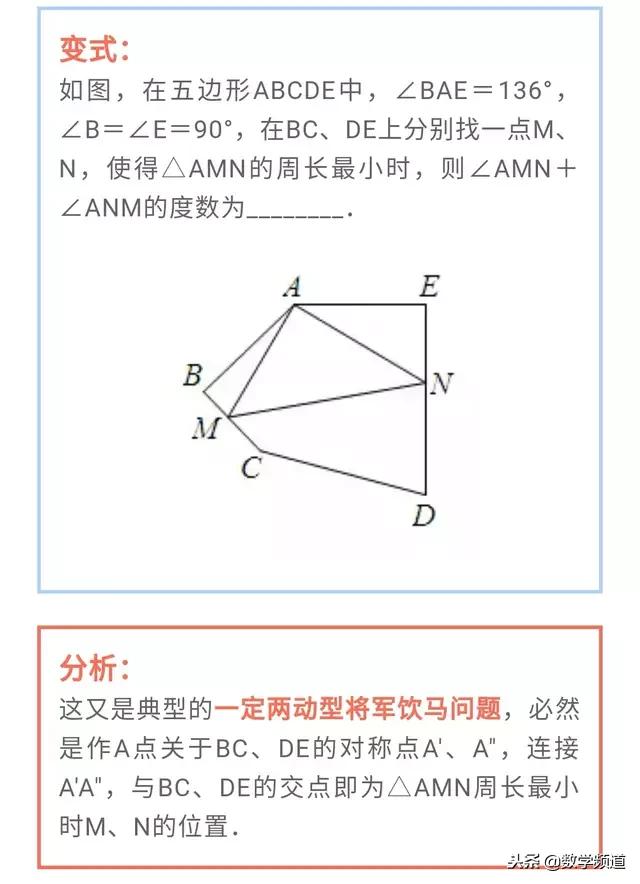
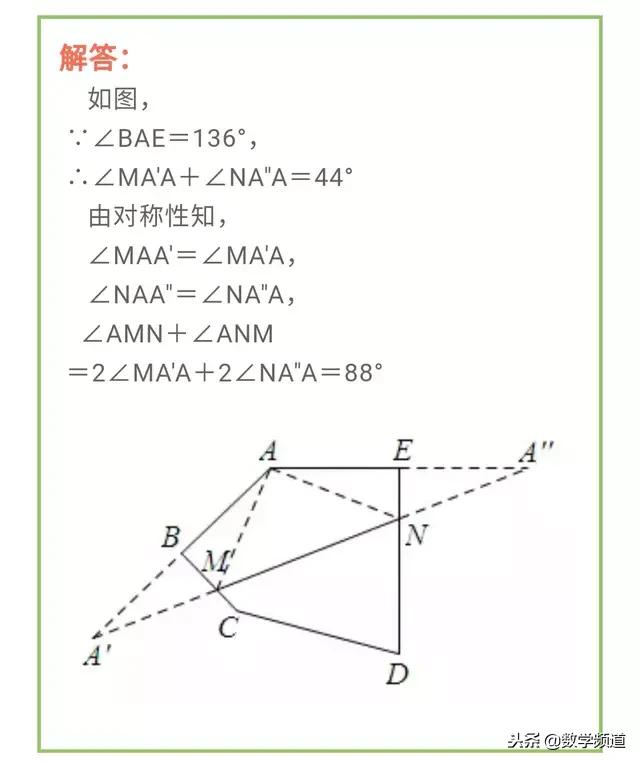
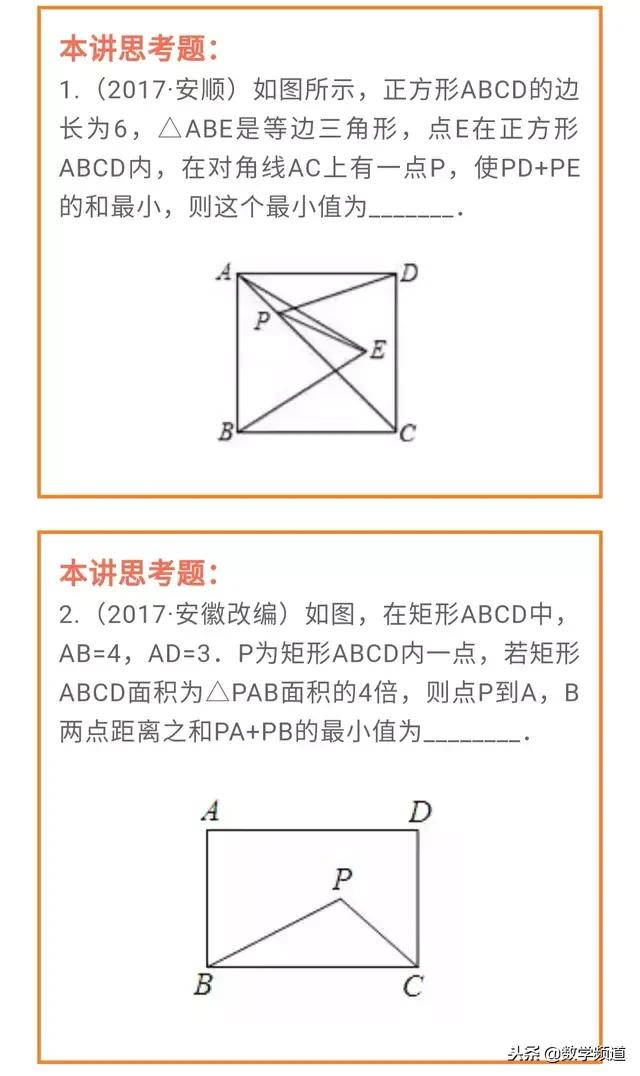
利用将军饮马模型求解角度最值问题，是将军饮马的一个另一个方向的应用。一直以来也是考察学生学以致用能力的常考题型。