
第四章节至第五章节知识点归纳及基础训练:
第四章 图形认识初步
【知识点归纳】
一、多姿多彩的图形
1. 从实物中抽象出的各种图形统称为几何图形。
2. 点、线、面、体
A.点:线和线相交的地方。
B.线:面和面相交的地方,线可分为直线、射线、线段
C.体:正方体、长方体、圆柱、球等都是几何体,几何体简称体。
D.面:包围着体的是面,面可分为平的面、曲的面。
二、直线、射线、线段
1.两点确定一条直线
2.当两条不同的直线有一个公共点时,我们就称这两条直线相交,
这个公共点叫做它们的交点。
3. 两点之间,线段最短。
4. 连接两点间的线段的长度,叫做这两点的距离。
三、角
1.有且只有一个角
2.把一个周角360等分,每一份就是一度的角,记做1°﹔把1度的角60等分,每一份叫做1分的角,记作1′﹔把1分的角60等分,每一份叫做1秒的角,记作1″。
3.角的运算:1周角=360°,1平角=180°,1°=60′,1′=60″
4.角的平分线:A. 从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的角平分线。
B.角平分线上的一点到角的两边距离相等。
四、线段、射线和直线的联系与区别
联系:线段、射线、直线是部分与整体的关系.线段向一方无限延长形成了射线,向两个方向无限延长得到了直线.直线上的两点和它们之间的部分组成线段,直线上的一点及其一旁的部分是射线,射线反向延长得直线.
区别:
名称延伸情况
有无长短图示表示法端点个数作图描述备注
线段不可延伸,有长短线段a或线段AB(BA) 2个连结AB A、B两点无序
射线向一个方向延伸,无长短射线AB 1个以A为端点作射线AB A、B两点有序,端点在前,射线上一点在后
直线向两个方向延伸直线l或直线AB(BA)无端点过A、B两点作直线AB A、B两点无序
【典型例题】
1.下列说法中,错误的有()
①射线是直线的一部分②画一条射线,使它的长度为3 cm ③线段AB和线段BA是同一条线段④射线AB和射线BA是同一条射线⑤直线AB和直线BA是同一条直线
A.1个 B.2个 C.3个 D.4个
【解析】B 线段与直线用两个大写字母表示时,两个字母的先后顺序可前可后,而射线必须是端点字母在前.
2.在同一平面内有A,B,C,D,E五点,任三点不在同一直线上,能画________条直线.
【答案】10
3.(1)田径运动中百米比赛的跑道是线段,起点与终点是它的两个端点.
(2)我们在晴朗的夜空中,有时能发现流星,它的运行轨迹可以近似看成直线.
【解析】(1)线段有两个端点.
(2)直线没有端点.
【典型习题】
4.下列说法中,错误的有( )
①射线是直线的一部分②画一条射线,使它的长度为3 cm③线段AB和线段BA是同一条线段④射线AB和射线BA是同一条射线⑤直线AB和直线BA是同一条直线
A.1个 B.2个 C.3个 D.4个
5.平面内三点,可确定的直线的条数为()
A.3 B.0或1 C.1或3 D.0
6.两点之间,____________最短.经过____________点有且只有一条直线.两点间的距离是指连接两点的____________.
7.作下面线段:
(1)有不在同一直线上的三点,每两点连一条线段,问可以连几条线段;
(2)有四个点,且每三点都不在同一直线上,每两点连一条线段,问可以连几条线段;
(3)用这个图形中的原理解决一个实际问题.
第五章节数据的收集、整理知识点汇总
一、总体、样本的概念
1.总体:要考察的全体对象称为总体.
2.个体:组成总体的每一个考察对象称为个体.
3.样本:被抽取的那些个体组成一个样本.
4.样本容量:样本中个体的数目叫样本容量(不带单位).
注意:为了使样本能较好地反映总体的情况,除了要有合适的样本容量外,抽取时还要尽量使每一个个体都有同等的机会被抽到.
二、全面调查与抽样调查
调查的方式有两种:全面调查和抽样调查:
1.全面调查:考察全面对象的调查叫全面调查. 全面调查也称作普查,调查的方法有:问卷调查、访问调查、电话调查等。
全面调查的步骤:(1)收集数据;(2)整理数据(划记法);(3)描述数据(条形图或扇形图等)。
2.抽样调查:若调查时因考察对象牵扯面较广,调查范围大,不宜采用全面调查,因此,采用抽样调查. 抽样调查只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况。
抽样调查的意义:
(1)减少统计的工作量;
(2)抽样调查是实际工作中应用非常广泛的一种调查方式,它是总体中抽取样本进行调查,根据样本来估计总体的一种调查.
3.判断全面调查和抽样调查的方法在于:
①全面调查是对考察对象的全面调查,它要求对考察范围内所有个体进行一个不漏的逐个准确统计;而抽样调查则是对总体中的部分个体进行调查,以样本来估计总体的情况. ②注意区分“总体”和“部分”在表述上的差异. 在调查实际生活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小。
4.频数分布直方图的画法:
(1)找到这一组数据的最大值和最小值;
(2)求出最大值与最小值的差;
(3)确定组距,分组;
(4)列出频数分布表;
(5)由频数分布表画出频数分布直方图。
5.画频数分布直方图的注意事项:
(1)分组时,不能出现数据中同一数据在两个组中的情况,为了避免,通常分组时,比题中要求数据单位多一位. 例如:题中数据要求到整数位,分组时要求数据到0.5即可。
(2)组距和组数的确定没有固定的标准,要凭借数据越多,分成的组数也就越多,当数据在100以内时根据数据的多少通常分成5~12组。
基础训练:


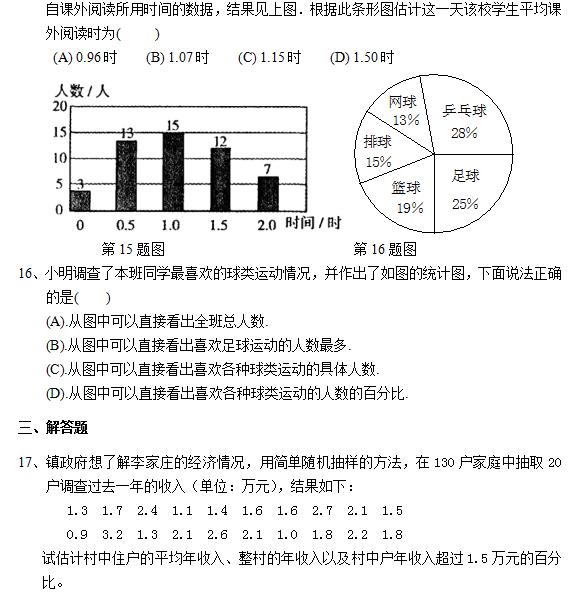
 加载中,请稍侯......
加载中,请稍侯......
精彩评论