函数概念并不难，理解“函”字是关键——函数概念如何理解

步入高中，数学科遇到的第一个拦路虎就是函数概念。

如下就是高中数学函数的概念：

学生读了函数的概念以后，往往是一头雾水。

在中国，函数一词是清代数学家李善兰（1811-1882）最初使用的。他在1859年与英国学者烈亚力（1815-1887）合译的《代数学》一书中，将“function”译作“函数”。老先生为什么给它取这么个名字呢？

函：即信也！老先生巧妙的用寄信来比喻函数，就是为了方便后来学习的人能够轻易理解函数的意义。那我们拿寄信来理解函数，就比较方便了！

顺着这个比喻往下理解，就很容易理解“使对于集合中的任意一个x，在集合中都有唯一一个确定的数f(x)和它对应”这句话了，就是说信x只能有一个收信人y，即f(x)，不可能一封信有多个收信地址的（清朝那时候没有群发功能）；而一个收信人却可以收到很多信，即一个x只能对应一个y，而一个y却能有多个x与之相对应。

其实，理解函数要理解两句话：

1）“A、B是两个非空数集”是指Ａ、B这两个集合不能有空集，而且这两个集合中的元素只能是数字，不能是其它的事物。

2）“对于集合A中的任意一个数x，在集合B中都有唯一确定的数分f(x)和它对应”是指A中的任意一个数x能且只能对应B中的一个数f(x)。

下面，给出几个例子:

【例题1】

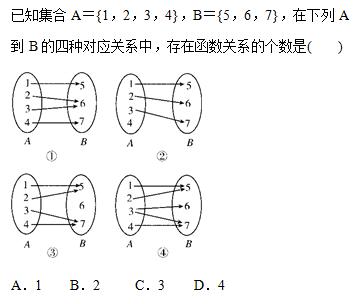
【解析】根据函数的定义可知，集合A中的每一个元素在B中都有唯一确定的实数与之对应.其中①③均满足函数定义.②A集合中的元素4在集合B中没有对应项，④A集合中的元素3在集合B中对应两项6和7，都不符合定义要求，所以不是函数.故选B.

【例题2】

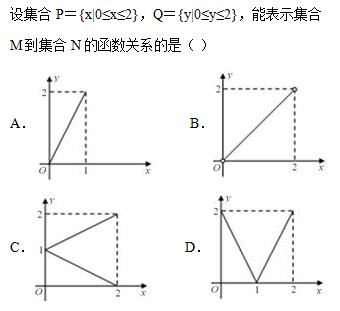
【解析】选项A中函数的定义域是[0,1]、B中函数的定义域是（0，2），都不是P，选项C中一个数x对应两个y值，不能构成函数，只有选项D符合函数的定义，故选D．

【例题3】

【解析】①M中有的元素在N中无对应元素．如M中的元素0；③M中的元素不是实数，即M不是数集；只有②满足函数的定义，故选A.

现在，你理解函数的概念了吗？