根据函数的概念，我们可以知道，所有的函数都有定义域，就是A集合。可是我们常常发现，很多题目给出的函数，只有解析式，没见定义域。这是何道理呢？其实，不写的，我们认为它的定义域为“默认定义域”！所谓默认定义域就是指“使得函数解析式中每个式子都有意义的自变量的取值集合”。

下面，我们就来说说求定义域的方法：

①解析式中含分式时：分母一定不为0；

②解析式中含偶次根号时：偶次根号下式子必须大于或等于0（非负数）；（奇次根号下式子无要求）

③解析式中含指数时：当指数为0时，底数一定不能为0（0°无意义）；

④解析式中含指数函数形式时：底数大于0且不等于1.（0<底数<1;底数>1）；

⑤解析式中含对数函数形式时：真数大于0，底数要大0且不等于1。（真数>0；0<底数<1;底数>1）

⑥解析式中含正切函数形式时：内函数不等于kπ+π/2

⑦当函数为复合函数时，外函数的定义域等于内函数的值域。

求函数定义域的时候，我们要观察函数的每一部分，仔细对照以上的7条，对上一个就写一个不等式。

函数最终的定义域就是以上所求的所有不等式的解集的交集。

【例题1】

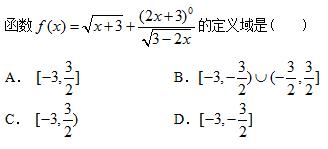
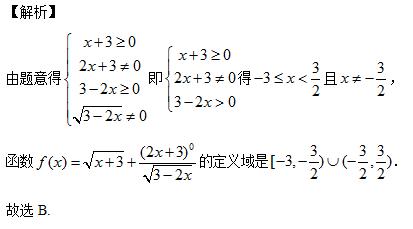
【例题2】

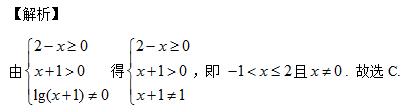
另外，还要遵循以下潜规则：

（1）所有式子都要注意观察，必须让所有的式子同时有意义。

（2）求定义域一定要在对函数解析式变形之前完成，不然会发生变化。例如：

(解析式一变形，定义域跟着变。）

（3）定义域是集合，所以最后的答案一定要写成集合或区间的形式，不能是范围。