抽象函数不用急，单调既定脱外衣——利用单调性解不等式

利用函数的单调性解不等式

过程：

（1）“常数”化成带“f( )”符号的函数值，不等号两侧，一侧有且仅有一个“函数符号f( )，且f( )前的符号必定为正号”

（2）要将各括号内的式子放入定义域内

（3）根据单调性脱去“函数符号f( )”，分两类：

增函数：函数值大自变量大，函数值小自变量小，不等号顺取。（增则顺）

减函数：函数值大自变量小，函数值小自变量大，不等号逆取。（减则逆）

典型例题：

典例1：f(x)是定义在(0，＋∞)上的单调增函数，满足f(xy)＝f(x)＋f(y)，f(3)＝1，当f(x)＋f(x－8)≤2时，x的取值范围是( )

A.(8，＋∞) B.(8,9] C.[8,9] D.(0,8)

关键词：函数f(x)的解析式没有给出，为抽象函数，且有不等式，求参数范围，关键词找到

分析：符号f( )在不等号两侧，每侧有且只有一个，所以利用题目性质，左侧f(x)＋f(x－8)可以化成f[x(x－8)]的形式，右侧的2=1＋1＝f(3)＋f(3)＝f(9)即化成带符号的函数值f(9)，再利用单调性脱去符号f( ).

解析：

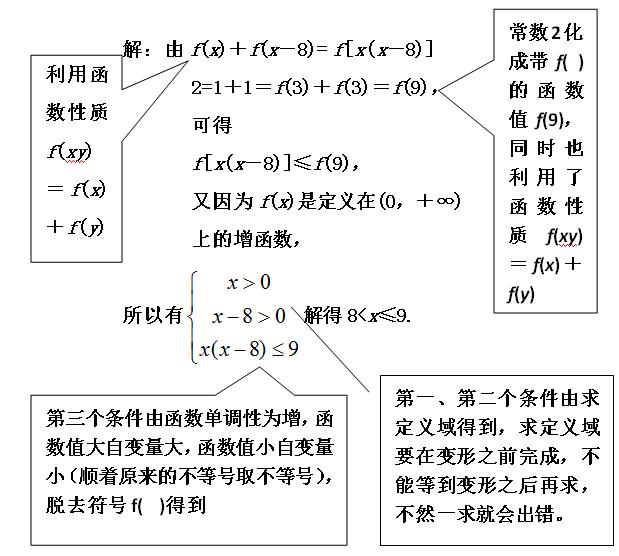
典例2：已知f(x)是定义域为(－1,1)的奇函数，而且f(x)是减函数，如果f(m－2)＋f(2m－3)>0，求实数m的取值范围.

解析