【今日目标】

1．学习并理解数轴的概念及三要素；

2．学习并理解有理数与数轴上的点的关系，并会借助数轴比较两个数的大小；

数轴

1.定义：规定了原点、正方向和单位长度的直线叫做数轴.

【要点诠释】

（1）原点、正方向和单位长度是数轴的三要素，三者缺一不可.

（2）长度单位与单位长度是不同的，单位长度是根据需要选取的代表“1”的线段，而长度单位是为度量线段的长度而制定的单位．有km、m、dm、cm等．

（3）原点、正方向、单位长度可以根据实际灵活选定，但一经选定就不能改动．

2. 数轴与有理数的关系：任何一个有理数都可以用数轴上的点来表示，但数轴上的点不都表示有理数，还可以表示其他数，比如 π.

【要点诠释】

（1）一般地，数轴上原点右边的点表示正数，左边的点表示负数；反过来也对，即正数用数轴上原点右边的点表示，负数用原点左边的点表示，零用原点表示.

（2）在数轴上表示的两个数，右边的数总比左边的数大.

1．如图所示是几位同学所画的数轴，其中正确的是 ( )

A．(1)(2)(3) B．(2)(3)(4) C．只有(2) D．(1)(2)(3)(4)

【答案】C

【解析】

对数轴的三要素掌握不清.（1）中忽略了单位长度，相邻两整点之间的距离不一致；（3）中负有理数的标记有错误；（4）图中漏画了表示方向的箭头.

【总结】

数轴是一条直线，可以向两端无限延伸；数轴的三要素：原点、正方向、单位长度缺一不可．

【变式】

如图为北京地铁的部分线路．假设各站之间的距离相等且都表示为一个单位长．现以万寿路站为原点，向右的方向为正，那么木樨地站表示的数为________，古城站表示的数为________；如果改以古城站为原点，那么木樨地站表示的数变为________．

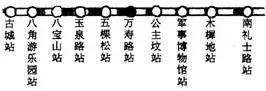
【答案】3，-5，8

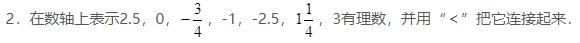
【解答】

【总结】

根据数轴的三要素先画好数轴，表示数的字母要依次对应有理数，然后根据在数轴上表示的两个数，右边的数总比左边的数大，比较大小．

【变式1】

（2014秋•埇桥区校级期中）有理数a、b在数轴上的位置如图所示，下列各式不成立的是（ ）

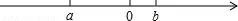
A．b﹣a＞0 B．﹣b＜0 C．﹣a＞﹣b D．﹣ab＜0

【答案】D

【变式2】

【答案】11；0，1，2，3

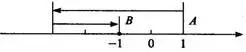
3．点A在数轴上，若将A向左移动4个单位长度，再向右移动2个单位长度，此时A点所表示的数是原来A点所表示的数的相反数，原来A点表示的是什么数?把你的研究过程在数轴上表示出来．

【思路】

根据数轴是以向右为正方向，故数的大小变化和平移变化之间的规律：左减右加．

【解答】

解：如图所示，B点表示A点移动后的位置．则AB＝2．因为A、B表示一对相反数．所以原点O是AB的中点，AO＝OB，所以A点表示1．

【总结】

先画出数轴，根据数轴理解题目中的数量关系，将有利于问题的解决.