【今日目标】

1．学会求一个数的相反数，并能借助数轴理解相反数的概念及几何意义；

2. 学习并掌握多重符号的化简.

相反数

1.定义：只有符号不同的两个数互为相反数；0的相反数是0.

【要点诠释】

（1）“只”字是说仅仅是符号不同，其它部分完全相同.

（2）“0的相反数是0”是相反数定义的一部分，不能漏掉.

（3）相反数是成对出现的，单独一个数不能说是相反数.

（4）求一个数的相反数，只要在它的前面添上“-”号即可.

2.性质：

（1）互为相反数的两数的点分别位于原点的两旁，且与原点的距离相等（这两个点关于原点对称）.

（2）互为相反数的两数和为0.

3.多重符号的化简

多重符号的化简，由数字前面“-”号的个数来确定，若有偶数个时，化简结果为正，如-{-[-(-4)]}=4 ；若有奇数个时，化简结果为负，如-{+[-(-4)]}=-4 .

【要点诠释】

　（1）在一个数的前面添上一个“＋”，仍然与原数相同，如＋5＝5，＋（－5）＝－5.

　（2）在一个数的前面添上一个“－”，就成为原数的相反数.如－（－3）就是－3的相反数，因此，－（－3）＝3.

1．（2015•宜宾）﹣1/5 的相反数是（ ）

A．5 B．1/5 C．﹣1/5 D.-5

【思路】

解决这类问题的关键是抓住互为相反数的特征“只有符号不同”，所以只要将原数的符号变为相反的符号，即可求出其相反数.

【答案】B

【总结】

求一个数的相反数，只改变这个数的符号，其他部分都不变.

【变式1】

【变式2】

下列说法中正确的有( )

①－3和＋3互为相反数；②符号不同的两个数互为相反数；③互为相反数的两个数必定一个是正数，一个是负数；④π的相反数是－3.14；⑤一个数和它的相反数不可能相等．

A. 0个 B.1个 C.2个 D.3个或更多

【答案】B

2．（2016•泰安模拟）如图，数轴上有A，B，C，D四个点，其中表示2的相反数的点是（ ）

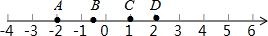
A．点A B．点B C．点C D．点D

【思路】

考查相反数的定义：只有符号不同的两个数互为相反数．根据定义，结合数轴进行分析．

【答案】A

【解析】

解：∵表示2的相反数的点，到原点的距离与2这点到原点的距离相等，并且与2分别位于原点的左右两侧，

∴在A，B，C，D这四个点中满足以上条件的是A．

故选A．

【总结】

本题考查了互为相反数的两个数在数轴上的位置特点：分别位于原点的左右两侧，并且到原点的距离相等．

3.化简下列各数中的符号．

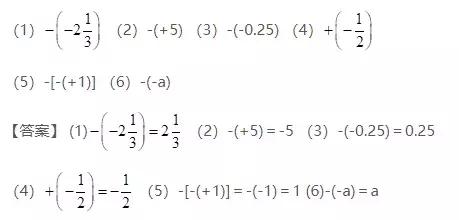
【解析】

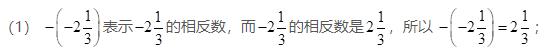
（2）-(+5)表示+5的相反数，即-5， 所以-(+5)=-5；

（3）-(-0.25)表示-0.25的相反数，而-0.25的相反数是0.25，所以-(-0.25)＝0.25；

（5）先看中括号内-(+1)表示1的相反数，即-1，因此-[-(+1)]＝-(-1)而-(-1)表示-1的相反数，即1，所以-[-(+1)]＝-(-1)=1；

(6)-(-a)表示-a的相反数，即a．所以-(-a)= a

【总结】

运用多重符号化简的规律解决这类问题较为简单．即数一下数字前面有多少个负号．若有偶数个，则结果为正；若有奇数个，则结果为负．