【今日目标】

1．借助数轴理解绝对值的概念，知道|a|的绝对值的含义；

2．会求一个数的绝对值，并会用绝对值比较有理数的大小；

3．通过应用绝对值解决实际问题，体会绝对值的意义和作用．

绝对值

1．定义：一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作|a|.

【要点诠释】

（1）绝对值的代数意义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．即对于任何有理数a都有：

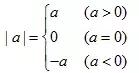
（2）绝对值的几何意义：一个数的绝对值就是表示这个数的点到原点的距离，离原点的距离越远，绝对值越大；离原点的距离越近，绝对值越小．

（3）一个有理数是由符号和绝对值两个方面来确定的．

2．性质：

（1）0除外，绝对值为一正数的数有两个，它们互为相反数．

（2）互为相反数的两个数的绝对值相等.

（3）绝对值具有非负性，即任何一个数的绝对值总是正数或0．

1．求下列各数的绝对值．

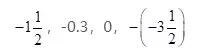
【思路】

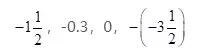
在数轴上位置距原点有多少个单位长度，这个数字就是各数的绝对值．还可以用绝对值法则来求解．

【解答】

方法1：

因为-0.3到原点距离是0.3个单位长度，所以|-0.3|＝0.3．

因为0到原点距离为0个单位长度，所以|0|＝0．

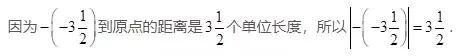
方法2：

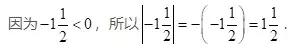
因为-0.3＜0，所以|-0.3|＝-(-0．3)＝0.3．

因为0的绝对值是它本身，所以|0|＝0

【总结】

求一个数的绝对值有两种方法：一种是利用绝对值的几何意义求解(如方法1)，一种是利用绝对值的代数意义求解(如方法2)，后种方法的具体做法为：首先判断这个数是正数、负数还是零．再根据绝对值的意义，确定去掉绝对值符号的结果是它本身，是它的相反数，还是零．从而求出该数的绝对值．

2．已知一个数的绝对值等于2009，则这个数是________．

【思路】

若一个数的绝对值是正数，则此数有两个，且互为相反数.

【答案】2009或-2009.

【解析】

根据绝对值的定义，到原点的距离是2009的点有两个，从原点向左侧移动2009个单位长度，得到表示数-2009的点；从原点向右侧移动2009个单位长度，得到表示数2009的点．

【总结】

已知绝对值求原数的方法：(1)利用概念；(2)利用数形结合法在数轴上表示出来．

【变式1】

（2015•镇江）已知一个数的绝对值是4，则这个数是 ．

【答案】±4.

【变式2】

如果｜x｜＝2，那么x＝_____ _ ；如果｜－x｜＝2，那么x＝______．

如果｜x－2｜＝1，那么x＝ ；如果｜x｜＞3，那么x的范围是 ．

【答案】+2或-2；+2或-2；1或3；x>3或x<3.

3.（2015•乐山期末）若|x﹣2|与|y+3|互为相反数，则x+y= ．

【思路】

由｜a｜≥0即绝对值的非负性可知，｜x﹣2｜≥0，｜y+3｜≥0，而它们的和为0．所以｜x﹣2｜＝0，|y+3|＝0．由此算出结果．

【答案】-1.

【解析】

∵|x﹣2|与|y+3|互为相反数，

∴|x﹣2|+|y+3|=0，

∴x﹣2=0，y+3=0，

解得x=2，y=﹣3，

∴x+y=2+（﹣3）=﹣1．

故答案为：﹣1．

【总结】

若几个数的绝对值的和为0，则每个数都等于0，即|a|+|b|+…+|m|＝0时，则a＝b＝…＝m＝0．