浙教版数学七上「每日一学」 有理数的大小比较

【今日目标】

1.学会并掌握多种比较有理数大小的方法。

有理数的大小比较

1．数轴法：

在数轴上表示出两个有理数，左边的数总比右边的数小． 如：a与b在数轴上的位置如图所示，则a＜b．

2．法则比较法：

两个数比较大小，按数的性质符号分类，情况如下：

【要点诠释】

利用绝对值比较两个负数的大小的步骤：（1）分别计算两数的绝对值；（2）比较绝对值的大小；（3）判定两数的大小．

3． 作差法：

设a、b为任意数，若a-b＞0，则a＞b；若a-b＝0，则a＝b；若a-b＜0，a＜b；反之成立．

4． 求商法：

设a、b为任意正数，若 a/b >1，则 a>b；若 a/b=1，则 a=b；若 a/b <1，则 a<b；反之也成立．若a、b为任意负数，则与上述结论相反．

5． 倒数比较法：

如果两个数都大于零，那么倒数大的反而小．

1. 在数轴上表示2.5，0，-3/4，-1，-2.5，5/4，3有理数，并用“＜”把它连接起来．

【解答】

如图所示，点A、B、C、D、E、F、G分别表示有理数2.5，0，-3/4，-1，-2.5，5/4，3．

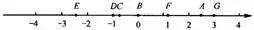
由上图可得：

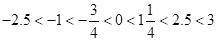
【总结】

根据数轴的三要素先画好数轴，表示数的字母要依次对应有理数，然后根据在数轴上表示的两个数，右边的数总比左边的数大，比较大小．

【变式1】

（2014秋•埇桥区校级期中）有理数a、b在数轴上的位置如图所示，下列各式不成立的是（ ）

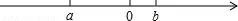
A．b﹣a＞0 B．﹣b＜0 C．﹣a＞﹣b D．﹣ab＜0

【答案】D

【变式2】

【答案】11；0，1，2，3

2．（2016春•上海校级月考）比较大小：|-7/4| -(-1.8)（填“＞”、“＜”或“=”）．

【思路】

先化简，再比较大小，即可解答．

【答案】＜．

【解析】

解：|-7/4|=7/4=1.75，-(-1.8)=1.8，

∵1.75＜1.8，

∴|﹣7/4|＜-(-1.8)，

故答案为：＜．

【总结】

本题考查了有理数大小比较，解决本题的关键是掌握绝对值的化简以及多重复号的化简方法．

【变式】

比大小：

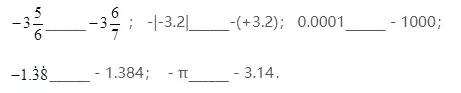
【答案】＞；=；＞；＞；＜.

3．在下列两数之间填上适当的不等号：

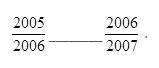
【思路】

根据“a-b＞0，a-b＝0，a-b＜0分别得到a＞b，a＝b，a＜b”来比较两数的大小．

【答案】＜

【解析】

法一：作差法

由于

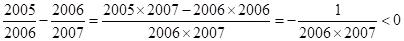
，所以

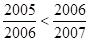
法二：倒数比较法

因为

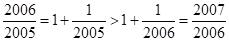
所以

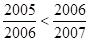
【总结】

比较大小常用的有五种方法，要根据数的特征选择使用．

【变式】

比较大小：(1)-1/99________0.001；(2)-2/3________-0.68

【答案】（1）＜ （2）＞