【今日目标】

1. 练习巩固用多种方法比较有理数大小。

有理数的大小比较

【知识链接】

1．数轴法：

在数轴上表示出两个有理数，左边的数总比右边的数小． 如：a与b在数轴上的位置如图所示，则a＜b．

2．法则比较法：

两个数比较大小，按数的性质符号分类，情况如下：

利用绝对值比较两个负数的大小的步骤：（1）分别计算两数的绝对值；（2）比较绝对值的大小；（3）判定两数的大小．

3． 作差法：

设a、b为任意数，若a-b＞0，则a＞b；若a-b＝0，则a＝b；若a-b＜0，a＜b；反之成立．

4． 求商法：

设a、b为任意正数，若 a/b >1，则 a>b；若 a/b=1，则 a=b；若 a/b <1，则 a<b；反之也成立．若a、b为任意负数，则与上述结论相反．

5． 倒数比较法：

如果两个数都大于零，那么倒数大的反而小．

一、选择题

1．（2016•娄底）已知点M、N、P、Q在数轴上的位置如图，则其中对应的数的绝对值最大的点是（ ）

A．M B．N C．P D．Q

2．若两个有理数a、b在数轴上表示的点如图所示，则下列各式中正确的是( )．

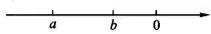
A．a＞b B．|a|＞|b| C．-a＜-b D．-a＜|b|

二、填空题

3.（2015•大邑县模拟）在﹣2.1，﹣2，0，1这四个数中，最小的数是 ．

4．数a在数轴上的位置如图所示．则|a-2|＝ ．

三、解答题

5．比较3a-2与2a+1的大小？

6．（2014秋•天水期末）如图，数轴上的三点A、B、C分别表示有理数a、b、c．

则：a﹣b 0，a+c 0，b﹣c 0．（用＜或＞或=号填空）

你能把|a﹣b|﹣|a+c|+|b﹣c|化简吗？能的话，求出最后结果．

一、选择题

1.【答案】D

【解析】解：∵点Q到原点的距离最远，

∴点Q的绝对值最大．

故选：D．

2．【答案】B

【解析】离原点越远的数的绝对值越大．

二、填空题

3.【答案】﹣2.1．

【解析】根据有理数比较大小的方法，可得﹣2.1＜﹣2＜0＜1.

4．【答案】a-2

【解析】由图可知：a≥2，所以|a-2|=a-2．

三、解答题

5．【解析】

解：(3a-2)-(2a+1)=3a-2-2a-1=a-3

当a>3时，3a-2>2a+1;

当a=3时，3a-2=2a+1;

当a<3时，3a-2<2a+1.

6.【解析】

解：由数轴得，

a﹣b＜0，a+c＜0，b﹣c＜0，

∴|a﹣b|﹣|a+c|+|b﹣c|=﹣（a﹣b）﹣[﹣（a+c）]+[﹣（b﹣c）]

=﹣a+b+a+c﹣b+c

=2c．