【今日目标】

1. 练习巩固绝对值的求解，并掌握用绝对值解决实际问题；

2. 巩固掌握绝对值的性质应用，并能用分类讨论思路解决问题。

绝对值的求解和性质应用

【知识链接】

（1）绝对值的代数意义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．即对于任何有理数a都有：

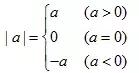
（2）绝对值的几何意义：一个数的绝对值就是表示这个数的点到原点的距离，离原点的距离越远，绝对值越大；离原点的距离越近，绝对值越小．

（3）一个有理数是由符号和绝对值两个方面来确定的．

（4）0除外，绝对值为一正数的数有两个，它们互为相反数．

（5）互为相反数的两个数的绝对值相等.

（6）绝对值具有非负性，即任何一个数的绝对值总是正数或0．

一、选择题

1．（2015.常州）-3的绝对值是（ ）．

A． 3 B．-3 C．1/3 D．-1/3

2．下列判断中，正确的是( )．

A. 如果两个数的绝对值相等，那么这两个数相等；

B. 如果两个数相等，那么这两个数的绝对值相等；

C.任何数的绝对值都是正数；

D.如果一个数的绝对值是它本身，那么这个数是正数.

3．下列各式错误的是( )．

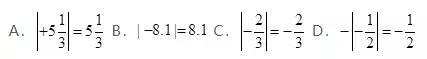
4．若|a| + a＝0，则a是( )．

A. 正数 B. 负数 C.正数或0 D.负数或0

二、填空题

5．若m，n互为相反数，则| m |________| n |；| m |=| n |，则m，n的关系是________．

6．已知| x |＝2，| y |＝5，且x＞y，则x＝________，y＝________．

7．满足3.5≤| x | ＜6的x的整数值是___________．

8．已知 |4x -3|=3-4x，则x的取值范围是________．

三、解答题

9．（2014秋•娄底期末）若有理数x、y满足|x|=5，|y|=2，且|x+y|=x+y，求x﹣y的值．

10．（2016春•桐柏县期末）若|a+1.2|+|b﹣1|=0，那么a+（﹣1）+（﹣1.8）+b等于多少？

一、选择题

1.【答案】A

2.【答案】B

【解析】A错误，因为两个数的绝对值相等，这两个数可能互为相反数；B正确；C错误，因为0的绝对值是0，而0不是正数；D错误，因为一个数的绝对值是它本身的数除了正数还有0.

3．【答案】C

【解析】因为一个数的绝对值是非负数，不可能是负数.所以C是错误的．

4. 【答案】D

【解析】若a为正数，则不满足|a| + a＝0；若a为负数，则满足|a| + a＝0；若a为0，也满足|a| + a＝0. 所以a≤0，即a为负数或0.

二、填空题

5. 【答案】=；m=±n

【解析】若m，n互为相反数，则它们到原点的距离相等，即绝对值相等；但反过来m，n绝对值相等，则它们相等或互为相反数.

6. 【答案】 ±2，-5

【解析】| x |＝2，则x=±2；| y |＝5， y=±5.但由于x＞y，所以x=±2，y=-5

7. 【答案】±4, ±5

【解析】画出数轴，从数轴上可以看出：在原点右侧，有4,5满足到原点的距离大于等于3.5，且小于6；在原点左侧有-4，-5满足到原点的距离大于等于3.5，且小于6.

8．【答案】x ≤ 3/4

【解析】将 4x-3 看成整体 a，即 |a|=-a，则 a≤0，故 4x-3≤0，x≤3/4．

三、解答题

9.【解析】

∵|x|=5，

∴x=±5，

又|y|=2，

∴y=±2，

又∵|x+y|=x+y，

∴x+y≥0，

∴x=5，y=±2，

当x=5，y=2时，x﹣y=5﹣2=3，

当x=5，y=﹣2时，x﹣y=5﹣（﹣2）=7．

10.【解析】

解：∵|a+1.2|+|b﹣1|=0，

∴a+1.2=0，b﹣1=0，

∴a=﹣1.2，b=1，

∴a+（﹣1）+（﹣1.8）+b=﹣3．